题目内容
如图所示,在电场强度E=5 N/C的匀强电场和磁感应强度B=2 T的匀强磁场中,沿平行于电场、垂直于磁场方向放一长绝缘杆,杆上套一个质量为m=10-4 kg,带电量q=2×10-4 C的小球,小球与杆间的动摩擦因数μ=0.2,小球从静止开始沿杆运动的加速度和速度各怎样变化?

答案:
解析:
解析:
|
解析:带电小球在竖直方向上受力平衡,开始沿水平方向运动的瞬间加速度: a1= 小球开始运动后加速度: a2=[qE-μ(mg-qvB)]/m,由于小球做加速运动,洛伦兹力F磁增大,摩擦力Ff逐渐减小,当mg=F磁时,Ff=0,加速度最大,其最大值为:a3= 随着速度v的增大,F磁>mg,杆对球的弹力N改变方向,又有摩擦力作用,其加速度:a4=[qE-μ(qvB-mg)]/m.可见Ff随v的增大而增大,a4逐渐减小.当Ff=F电时,加速度a5=0,此时速度最大,此后做匀速运动. 由qE=μ(qvB-mg)解得v=15 m/s. 结论:小球沿杆运动的加速度由8 m/s2逐渐增大到10 m/s2,接着又逐渐减小到零,最后以15 m/s的速度做匀速运动 |

练习册系列答案
相关题目
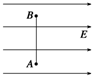 如图所示,在电场强度为E、方向水平向右的匀强电场中,A、B为一竖直线上的两点,相距为L,外力F将质量为m、带电荷量为q的粒子从A点匀速移到B点,重力不能忽略,则下列说法中正确的是( )
如图所示,在电场强度为E、方向水平向右的匀强电场中,A、B为一竖直线上的两点,相距为L,外力F将质量为m、带电荷量为q的粒子从A点匀速移到B点,重力不能忽略,则下列说法中正确的是( )| A、外力的方向水平向左 | ||
| B、外力的方向竖直向上 | ||
| C、外力的大小等于qE+mg | ||
D、外力的大小等于
|
 如图所示,在电场强度为E的水平匀强电场中,有一长为L,质量可以忽略不计的绝缘杆,可绕通过杆中点并与电场强度方向垂直的水平轴O在竖直平面内转动(轴间摩擦不计).杆的两端各固定一个小球A和B,它们的质量分别为2m和m,电量分别为2Q和-Q.开始时,杆处在图中所示的竖直位置,然后放手,杆发生转动,求杆转过900到达水平位置时A球的动能.
如图所示,在电场强度为E的水平匀强电场中,有一长为L,质量可以忽略不计的绝缘杆,可绕通过杆中点并与电场强度方向垂直的水平轴O在竖直平面内转动(轴间摩擦不计).杆的两端各固定一个小球A和B,它们的质量分别为2m和m,电量分别为2Q和-Q.开始时,杆处在图中所示的竖直位置,然后放手,杆发生转动,求杆转过900到达水平位置时A球的动能. (2012?通州区模拟)如图所示,在电场强度为E的匀强电场中,一个电荷量为q的正点电荷,沿电场线方向从A点运动到B点,A、B两点间的距离为d.在此过程中电场力对电荷做的功等于( )
(2012?通州区模拟)如图所示,在电场强度为E的匀强电场中,一个电荷量为q的正点电荷,沿电场线方向从A点运动到B点,A、B两点间的距离为d.在此过程中电场力对电荷做的功等于( ) (2010?黑龙江模拟)如图所示,在电场强度为2.0×102V/m的匀强电场中,A、B两点相距0.30m,则A、B两点间的电势差为
(2010?黑龙江模拟)如图所示,在电场强度为2.0×102V/m的匀强电场中,A、B两点相距0.30m,则A、B两点间的电势差为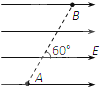 如图所示,在电场强度E=5×105V/m的匀强电场中,将一电荷量q=2×10-5C的正电荷由A点移到B点,已知A、B两点间距离为2cm,两点连线与电场方向成60°角,求:
如图所示,在电场强度E=5×105V/m的匀强电场中,将一电荷量q=2×10-5C的正电荷由A点移到B点,已知A、B两点间距离为2cm,两点连线与电场方向成60°角,求: