题目内容
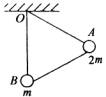
如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球.支架悬挂在O点，可绕过O点并与支架所在平面相垂直的固定轴转动，开始时OB与地面相垂直.放手后开始运动，在不计任何阻力的情况下，下列说法正确的是 [ ]A.A球到达最低点时速度为零
B.A球机械能减少量等于B球机械能增加量
C.B球向左摆动所能达到的最高位置应高于A球开始运动时的高度
D.当支架从右向右回摆时，A球一定能回到起始高度
答案：BCD
解析：
提示：
解析：
因A处小球质量大，处的位置高，图示中三角形框架处于不稳定状态，释放后支架就会向左摆动.摆动过程中只有小球受的重力做功，故系统的机械能守恒，选项B正确，D选项也正确.A球到达最低点时，若设支架边长是L，A球下落的高度便是 ，有 的重力势能转化为支架的动能，因而此时，A球速度不为零，选项A错.当A球到达最低点时有向左运动的速度，还要继续左摆，B球仍要继续上升，因此B球能达到的最高位置比A球的最高位置要高，C选项也正确.答案BCD.
|
提示：
| 功能关系的应用，使用机械能守恒定律
|
练习册系列答案
相关题目
（2000?上海）如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球．支架悬挂在O点，可绕O点并与支架所在平面相垂直的固定轴转动．开始时OB与地面相垂直，放手后开始运动，在不计任何阻力的情况下，下列说法正确的是（ ）
如图所示，长度相同的三根轻杆构成一个正三角形支架，在A处固定质量为2m的小球，B处固定质量为m的小球，支架悬挂在O点，可绕过点O并与支架所在平面垂直的固定轴转动，开始时OA与地面垂直，放手后开始运动，在不计任何阻力的情况下，下列说法正确的是（ ）
如图所示，长度相同的三根轻杆构成一个正三角形支架，固 定质量为2m的小球A，质量为m的小球B，支架悬挂在O点，可绕过O点并与支架所在平面相垂直的固定轴转动．开始时OB与地面相垂直．放手后开始运动，在不计任何阻力的情况下，下列说法不正确的是（ ）
如图所示，长度相同的l轻杆构成一个直角形支架，在A端固定质量为2m的小球，B端固定质量为m的小球，支架可绕O点在竖直面内自由旋转．现从OB竖直、OA水平，静止释放支架，下列说法中正确的是（ ）A、A球到达最低点时速度为
| ||||
B、从开始到 A球到达最低点的过程中，支架对B球做的功为
| ||||
| C、当支架下摆45°时（A、B两球等高时），A球速度最大 | ||||
| D、当支架从左向右返回摆动时，A球一定能回到起始高度 |