题目内容
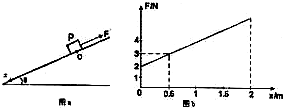 如图a所示,有一个足够长的光滑斜面,倾角θ为30°,质量为0.8kg的物体置于O处.物体受到一个沿斜面向上的拉力F作用下由静止开始运动,F与x的关系如图b所示,x为物体相对于O点的位移,x轴正方向沿斜面向下,如图a所示,则:
如图a所示,有一个足够长的光滑斜面,倾角θ为30°,质量为0.8kg的物体置于O处.物体受到一个沿斜面向上的拉力F作用下由静止开始运动,F与x的关系如图b所示,x为物体相对于O点的位移,x轴正方向沿斜面向下,如图a所示,则:(1)当物体位移x=0.5m时物体的加速度为多大?方向如何?
(2)当物体位移x为多大时物体的加速度最大?最大值为多少?
(3)当物体位移x为多大时物体的速度最大?最大值为多少?
分析:(1)对物体受力分析,受重力、支持力和拉力,根据牛顿第二定律列式求解;
(2)受力分析后得出合力的一般表达式,再根据牛顿第二定律求解出加速度的最大值;
(3)物体先加速下降后加速上升,通过第1m的位移内,物体做加速度不断减小的加速运动,第2m的位移内,物体做加速度不断变大的减速运动对第1m过程运用动能定理列式求解.
(2)受力分析后得出合力的一般表达式,再根据牛顿第二定律求解出加速度的最大值;
(3)物体先加速下降后加速上升,通过第1m的位移内,物体做加速度不断减小的加速运动,第2m的位移内,物体做加速度不断变大的减速运动对第1m过程运用动能定理列式求解.
解答:解:(1)由图b可知:F=2+2x,当x=0.5m时,F=3N
根据牛顿定律:a=
=
m/s2=1.25m/s2
加速度a的方向:沿斜面向下.
(2)∵根据受力分析可知F合=mgsinθ-F=0.8×10×0.5-(2+2x)=2-2x
∴物体P以x=1m为平衡位置,沿x轴做机械振动.
∴x=0处,加速度最大,amax=
m/s2=2.5m/s2
x=2m处,加速度最大,amax=
m/s2=-2.5m/s2
(上式中负号表示加速度的方向沿x轴的负方向)
(3)∵x=1m处,F合=0,a=0
∴x=1m处速度最大,且设为vm
又∵从x=0到x=1m的过程中根据动能定理可得:
mg△xsinθ-
△x=
m
-0
其中F0=2N,F1=4N,△x=1m
带入数据:0.8×10×1×0.5-
=
×0.8×
解得:vm=
m/s=1.58m/s
即当物体位移x为1m时物体的速度最大,最大值为1.58m/s.
根据牛顿定律:a=
| mgsinθ-F |
| m |
| 0.8×10×0.5-3 |
| 0.8 |
加速度a的方向:沿斜面向下.
(2)∵根据受力分析可知F合=mgsinθ-F=0.8×10×0.5-(2+2x)=2-2x
∴物体P以x=1m为平衡位置,沿x轴做机械振动.
∴x=0处,加速度最大,amax=
| 2-2×0 |
| 0.8 |
x=2m处,加速度最大,amax=
| 2-2×2 |
| 0.8 |
(上式中负号表示加速度的方向沿x轴的负方向)
(3)∵x=1m处,F合=0,a=0
∴x=1m处速度最大,且设为vm
又∵从x=0到x=1m的过程中根据动能定理可得:
mg△xsinθ-
| F0+F1 |
| 2 |
| 1 |
| 2 |
| v | 2 m |
其中F0=2N,F1=4N,△x=1m
带入数据:0.8×10×1×0.5-
| 2+4 |
| 2 |
| 1 |
| 2 |
| v | 2 m |
解得:vm=
| ||
| 2 |
即当物体位移x为1m时物体的速度最大,最大值为1.58m/s.
点评:本题关键是对物体受力分析,得到加速度,然后判断物体的运动情况,最后根据动能定理列式求解.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目






