题目内容
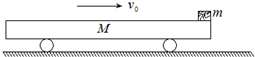如图所示，一辆长L=2m、高h=0.8m、质量为M=12kg的平顶车，车顶面光滑，车与水平长直路面间的动摩擦因数μ=0.3，车在路面上无动力的滑行，当车速为v0=7m/s时，把一个质量为m=1kg的物块（视为质点）轻轻放在车顶的前端．从物块放上车开始计时，求（1）物块经过多长时间着地？
（2）经过3s时间，物块离车前端多远？（物块着地后不再反弹，取g=10m/s2，计算结果保留2位有效数字）
分析：由于m与M无摩擦，所以开始物块m在车上静止，离开车后做自由落体运动，物块经历的时间为小车匀减速运动L的时间与物块自由落体运动的时间之和；
物块离车前端的距离为车长加上物块自由落体时间内前进的距离．
物块离车前端的距离为车长加上物块自由落体时间内前进的距离．
解答：解：由于m与M无摩擦，所以开始物块m在车上静止，离开车后做自由落体运动，
放上m后地面对M的摩擦力F1=μ（m+M）g，则M的加速度
a1═μg（1+
）=3.25 m/s2
m离开M前，M做减速运动，位移s1=L，设m即将落地时车速度为v，则由运动学公式
v02-v2=2a1L，得v═6 m/s
物块m下落时间t=
=s=0.4 s
物块在车上的时间为：t′=
≈0.31s
则从物块放上车开始计时至落地的时间t总=t+t′=0.71s
m离开M后，M的加速度a2═μg=3 m/s2
在0.4 s内车前进的距离s2=v t-
a2t2=2.16 m
所以，物体落地点离车前端距离s=s2+L=2.16 m+2 m=4.16 m
答：（1）物块经过0.71s着地；
（2）经过3s时间，物块离车前端4.16m．
放上m后地面对M的摩擦力F1=μ（m+M）g，则M的加速度
a1═μg（1+
| m |
| M |
m离开M前，M做减速运动，位移s1=L，设m即将落地时车速度为v，则由运动学公式
v02-v2=2a1L，得v═6 m/s
物块m下落时间t=
|
物块在车上的时间为：t′=
| 7-6 |
| 3.25 |
则从物块放上车开始计时至落地的时间t总=t+t′=0.71s
m离开M后，M的加速度a2═μg=3 m/s2
在0.4 s内车前进的距离s2=v t-
| 1 |
| 2 |
所以，物体落地点离车前端距离s=s2+L=2.16 m+2 m=4.16 m
答：（1）物块经过0.71s着地；
（2）经过3s时间，物块离车前端4.16m．
点评：本题考查牛顿第二定律与运动学公式的综合运用问题，关键是注意滑块滑落前后小车加速度大小的变化情况．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一辆长L=3.6m，高h=1.8m，车顶光滑的平顶车，驾驶员在关闭发动机后让汽车做减速运动，已知车的加速度大小恒为0.2m/s2，当车速为v0=2m/s时，把一个质量为m=1kg的滑块（视为质点）轻轻放在车顶的前端，问：
（2005?诸城市模拟）如图所示，一辆长L=2m、高h=0.8m、质量为M=12kg的平顶车，车顶光滑，在牵引力为零时，仍在向前运动，车与路面间的动摩擦因数μ=0.3．当车速为v0=7m/s时，把一个质量为m=1kg的物块（视为质点）轻轻放在车顶的前端．问物块落地时，落地点距车前端多远？（取g=10m/s2．）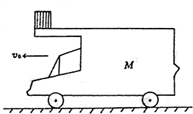
如图所示，一辆长L=2m，高 h=0.8m，质量为 M=12kg 的平顶车，车顶面光滑，在牵引力为零时，仍在向前运动，设车运动时受到的阻力与它对地面的压力成正比，且比例系数μ=0.3．当车速为 v0=7m/s 时，把一个质量为 m=1kg 的物块（视为质点）轻轻放在车顶的前端，并开始计时．那么，经过t=