题目内容
如图所示的是杂技演员表演的“水流星”.一根细长绳的一端,系着一个盛了水的容器.以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动.N为圆周的最高点,M为圆周的最低点.若“水流星”通过最低点时的速度v=
.则下列判断正确的是( )

| 5gR |
| A.“水流星”到最高点时的速度为零 |
| B.“水流星”通过最高点时,有水从容器中流出 |
| C.“水流星”通过最高点时,水对容器底没有压力 |
| D.“水流星”通过最高点时,绳对容器有向下的拉力 |

A、根据动能定理得,-mg?2R=
mv′2-
mv2,解得最高点的速度v′=
.故A错误.
B、对桶中的水分析,有N+mg=m
,解得N=0.知水对桶底压力恰好为零,水恰好不流出.故B错误,C正确.
D、对整体受力分析,有:F+mg=m
,解得F=0,绳子的拉力为零.故D错误.
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
| gR |
B、对桶中的水分析,有N+mg=m
| v′2 |
| R |
D、对整体受力分析,有:F+mg=m
| v′2 |
| R |
故选C.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
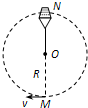 (2007?西城区模拟)如图所示的是杂技演员表演的“水流星”.一根细长绳的一端,系着一个盛了水的容器.以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动.N为圆周的最高点,M为圆周的最低点.若“水流星”通过最低点时的速度
(2007?西城区模拟)如图所示的是杂技演员表演的“水流星”.一根细长绳的一端,系着一个盛了水的容器.以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动.N为圆周的最高点,M为圆周的最低点.若“水流星”通过最低点时的速度 如图所示的是杂技演员表演的“水流星”.一根细长绳的一端,系着一个盛了水的容器.以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动.N为圆周的最高点,M为圆周的最低点.若“水流星”通过最高点时绳子的拉力恰为mg,则下列判断错误的是( )
如图所示的是杂技演员表演的“水流星”.一根细长绳的一端,系着一个盛了水的容器.以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动.N为圆周的最高点,M为圆周的最低点.若“水流星”通过最高点时绳子的拉力恰为mg,则下列判断错误的是( ) 。则下列判断正确的是( )
。则下列判断正确的是( )


 .则下列判断正确的是( )
.则下列判断正确的是( )