题目内容
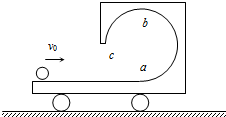
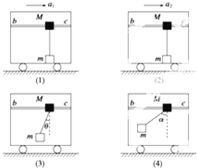 如图所示,一辆小车静止在水平地面上,bc是固定在小车上的水平横杆,物块M穿在杆上,M通过线悬吊着小物体m,m在小车的水平底板上,小车未动时,细线恰好在竖直方向上,现使车向右运动,全过程中M始终未相对杆bc移动,M、m与小车保持相对静止,已知a1:a2:a3:a4=1:2:4:8,M受到的摩擦力大小依次为 f1、 f2、 f3、 f4,则以下结论正确的是( )
如图所示,一辆小车静止在水平地面上,bc是固定在小车上的水平横杆,物块M穿在杆上,M通过线悬吊着小物体m,m在小车的水平底板上,小车未动时,细线恰好在竖直方向上,现使车向右运动,全过程中M始终未相对杆bc移动,M、m与小车保持相对静止,已知a1:a2:a3:a4=1:2:4:8,M受到的摩擦力大小依次为 f1、 f2、 f3、 f4,则以下结论正确的是( )| A、 f1: f2=1:2 | B、 f2: f3=1:2 | C、 f3: f4=1:2 | D、tanα=2tanθ |
分析:前两图中,M是由静摩擦力提供加速度的,根据牛顿第二定律直接求解f1和f2的关系;后两图中对小球和滑块整体受力分析,根据牛顿第二定律列式求解.通过对m隔离分析可判断图中角的关系.
解答: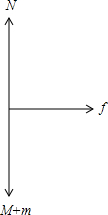 解:甲乙两图中,M水平方向只受静摩擦力作用,根据牛顿第二定律得:
解:甲乙两图中,M水平方向只受静摩擦力作用,根据牛顿第二定律得:
f1=Ma1
f2=Ma2
丙丁两图中,对m和M整体受力分析,受总重力(M+m)g、支持力N、摩擦力f,
如图所示:
根据牛顿第二定律,有:f=(M+m)a;
即f3=(M+m)a3,f4=(M+m)a4
又:a1:a2=1:2,则:f1:f2=1:2,故A正确;
a2:a3=2:4,f2:f3=M:2(M+m),故B错误;
f3:f4=a3:a4=4:8=1:2,故C正确;
对物体m隔离受力分析,可得tanθ=
,tanα=
,而a3:a4=4:8,所以 tanα=2tanθ,故D正确.
故选:ACD.
 解:甲乙两图中,M水平方向只受静摩擦力作用,根据牛顿第二定律得:
解:甲乙两图中,M水平方向只受静摩擦力作用,根据牛顿第二定律得:f1=Ma1
f2=Ma2
丙丁两图中,对m和M整体受力分析,受总重力(M+m)g、支持力N、摩擦力f,
如图所示:
根据牛顿第二定律,有:f=(M+m)a;
即f3=(M+m)a3,f4=(M+m)a4
又:a1:a2=1:2,则:f1:f2=1:2,故A正确;
a2:a3=2:4,f2:f3=M:2(M+m),故B错误;
f3:f4=a3:a4=4:8=1:2,故C正确;
对物体m隔离受力分析,可得tanθ=
| a3 |
| g |
| a4 |
| g |
故选:ACD.
点评:本题关键是对滑块、滑块与小球整体受力分析后根据牛顿第二定律列式求解,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某人拍得一张照片,上面有一个倾角为α的斜面,斜面上有一辆小车,小车上悬挂一个小球,如图所示小车自由放在斜面上,小球悬线与垂直斜面的方向夹角为β,下面判断正确的是( )
| A.如果β=α,小车一定处于静上状态 |
| B.如果β=0,斜面一定是光滑的 |
| C.如果β>α,小车一定是加速向下运动 |
| D.无论小车做什么运动,悬线都不可能停留图中虚线的右侧 |
 (2012?静安区一模)AB是一条平直公路边上的两块路牌,一辆匀速行驶的小车由右向左经过B路牌时,一只小鸟恰自A路牌向B匀速飞去,小鸟飞到小车正上方立即折返,以原速率飞回A,过一段时间后,小车也行驶到A.它们的位置与时间的关系如图所示,图中t2=2t1,由图可知( )
(2012?静安区一模)AB是一条平直公路边上的两块路牌,一辆匀速行驶的小车由右向左经过B路牌时,一只小鸟恰自A路牌向B匀速飞去,小鸟飞到小车正上方立即折返,以原速率飞回A,过一段时间后,小车也行驶到A.它们的位置与时间的关系如图所示,图中t2=2t1,由图可知( )