题目内容
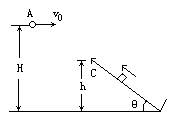
如图所示，质量M＝0.45kg的带有小孔的塑料块沿斜面上滑动最高点C时速度恰为零，此时与从A点水平射出的弹丸相碰，弹丸沿着斜面方向进入塑料块中，并立即与塑料块有相同的速度．已知A点和C点距地面的高度分别为：H＝1.95m，h＝0.15m，弹丸的质量m＝0.050kg，水平初速度v0＝8m/s．取g＝10m/s2求：
(1)斜面与水平地面的夹角θ；(可用反三角函数表示)
(2)若在斜面下端与地面交接处设一个垂直于斜面的弹性挡板，塑料块与它相碰后的速率等于碰前的速率，要使塑料块能够反弹回到C点，斜面与塑料块间的动摩擦因数可为多少？
解析：
|
解：(1)弹丸做平抛运动，经时间t有：
H－h＝ 解出： t＝0.6s 此时弹丸的速度与水平方向夹角为θ，水平分速度为vx、竖直分速度为vy则有：
vx＝v0，vy＝g t，tanθ＝ 解出： tanθ＝ 由于弹丸沿斜面方向与塑料块相碰，故外面的倾角与t秒末弹丸的速度与水平方向的夹角相同，所以斜面的倾角
θ＝arctan (2)设在C点弹丸的末速度为vt，则有：
所以，
vt＝ 弹丸立即打入塑料块，满足动量守恒条件，有： mvt＝(m＋M)vc，解得vc＝1m/s． 碰后，弹丸与塑料块共同运动由C点到与挡板碰撞并能够回到C点，有：
Wf＝2fs＝2sμ(M＋m)gcosθ．s＝ 代入数据得：μ≤0.125，弹丸与塑料块共同运动要能够回到C点：μ≤0.125． |
gt2
，
，∴θ＝arctan
．
，
＝10m/s．
＝
；
；
Wf．
．
（取g＝10m/s2）。
