题目内容
(1)一列简谐横波,沿x轴正向传播,t1=0和t2=0.25s两个时刻的波形图如图1所示,求该波的传播速度的可能值.(2)如图2,一玻璃柱体的横截面为半圆形,细的单色光束从空气射向柱体的O点(半圆的圆心),产生反射光束1和透射光束2,已知玻璃折射率为
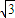 ,当入射角i=60°时,求反射光束1和透射光束2之间的夹角多大?
,当入射角i=60°时,求反射光束1和透射光束2之间的夹角多大?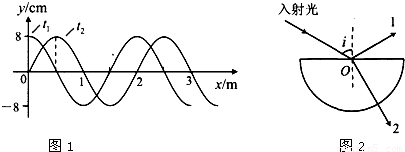
【答案】分析:(1)根据两时刻的波形,确定时间与周期的关系,得到传播距离x的通项式,由v=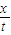 得到该波的传播速度的通项;
得到该波的传播速度的通项;
(2)根据反射定律得到反射角,由折射定律求出折射角,即可由几何关系得到反射光束1和透射光束2之间的夹角.
解答:解:
(1)由图可知,该波在t1到t2的时间内,传播的距离为 x=(0.5+2n)m(n=0,1,2,…)①
因此,该波的传播速度的可能值为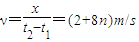 (n=0,1,2,…)②
(n=0,1,2,…)②
(2)根据反射定律得:反射角i'=i=60°③
由折射定律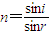 ④
④
解得折射角r=30°⑤
因此反射光束1和透射光束2之间的夹角θ=180°-(i'+r)=90°⑥
答:(1)该波的传播速度的可能值是(2+8n)m/s(n=0,1,2,3…).
(2)反射光束1和透射光束2之间的夹角为90°.
点评:第1题关键要抓住波的空间周期性得到波的传播距离表达式;第2题关键要掌握反射定律和折射定律.
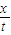 得到该波的传播速度的通项;
得到该波的传播速度的通项;(2)根据反射定律得到反射角,由折射定律求出折射角,即可由几何关系得到反射光束1和透射光束2之间的夹角.
解答:解:
(1)由图可知,该波在t1到t2的时间内,传播的距离为 x=(0.5+2n)m(n=0,1,2,…)①
因此,该波的传播速度的可能值为
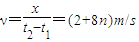 (n=0,1,2,…)②
(n=0,1,2,…)②(2)根据反射定律得:反射角i'=i=60°③
由折射定律
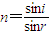 ④
④解得折射角r=30°⑤
因此反射光束1和透射光束2之间的夹角θ=180°-(i'+r)=90°⑥
答:(1)该波的传播速度的可能值是(2+8n)m/s(n=0,1,2,3…).
(2)反射光束1和透射光束2之间的夹角为90°.
点评:第1题关键要抓住波的空间周期性得到波的传播距离表达式;第2题关键要掌握反射定律和折射定律.

练习册系列答案
相关题目




 (1)一列简谐横波在t1=0时刻的波形图象如图甲所示,此时波中的质点M正处于平衡位置,且沿y轴负方向运动.到t2=0.7s时质点M恰好第二次到达y轴正方向最大位移处.试确定该波传播方向并求波速大小.
(1)一列简谐横波在t1=0时刻的波形图象如图甲所示,此时波中的质点M正处于平衡位置,且沿y轴负方向运动.到t2=0.7s时质点M恰好第二次到达y轴正方向最大位移处.试确定该波传播方向并求波速大小.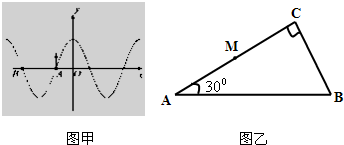 物理 选修3-4
物理 选修3-4