题目内容
如图所示，在水平向左的匀强电场中，一根不可伸长的绝缘细线长度为L，一端拴一个质量为m电荷量为q的带负电小球，另一端固定在O点．把小球拉到使细线水平伸直的位置A然后将小球由静止释放，小球沿弧线运动到细线与水平方向成θ=60°的位置B时速度为零．则电场强度E= ，小球运动过程中的最大速率为 ．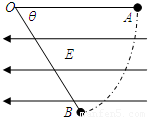
【答案】分析：小球在下落过程中有重力和电场力做功，则由动能定理可求得电场强度；由OB摆过的角度利用动能定理可以表示出速度的表达式，由数学关系要得出最大速率．
解答：解：由动能定理可知：
mgLsin60°-EqL（1-cos60°）=0
解得：E=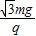
；
设小球在运动中细线与水平方向的夹角为α，则对任一时刻应有：
mgLsinα-EqL（1-cosα）=
mv2；
解得：v=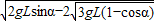
=
=
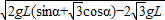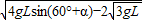
当α=30°时，v最大，最大值vm=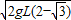
；
故答案为：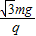
；
．
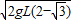点评：本题要注意电场力与重力做功的特点，二力做功均与路径无关；
本题采用了数学方法求解；而在解题时还可以应用物理分析法求解，先分析二力的合力方向，则可知，在当小球运动到该方向时速度最大．
解答：解：由动能定理可知：
mgLsin60°-EqL（1-cos60°）=0
解得：E=
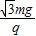；设小球在运动中细线与水平方向的夹角为α，则对任一时刻应有：
mgLsinα-EqL（1-cosα）=
mv2； 解得：v=
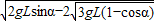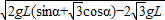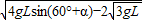
==当α=30°时，v最大，最大值vm=
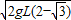； 故答案为：
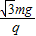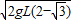；．点评：本题要注意电场力与重力做功的特点，二力做功均与路径无关；
本题采用了数学方法求解；而在解题时还可以应用物理分析法求解，先分析二力的合力方向，则可知，在当小球运动到该方向时速度最大．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在水平向左的匀强电场中，一带电小球用绝缘轻绳（不可伸缩）悬于O点，平衡时小球位于A点，此时绳与竖直方向的夹角θ=53°，绳长为L，图中BD水平，OC竖直．BO=CO=DO=L．
如图所示，在水平向左的场强E=5×104V/m的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC，其下端（C端）距地面高度h=0.8m．有一质量为500g的带电小环套在直杆上，正以某一速度v0沿杆匀速下滑，小环离开杆后正好通过C端的正下方P点处．（g取l0m/s2）求：
如图所示，在水平向左的匀强电场中，一根细线一端系一个质量为m的带正电的小球，另一端固定在O点．现在让细线水平绷直，小球从A点由静止开始摆下，小球能达到并通过最低点B．则小球在最低点B处细线的拉力可能是（ ）
如图所示，在水平向左的匀强电场中，一根长为L且不可伸长的绝缘细线一端拴一个质量为m带负电的小球，另一端固定在O点．把小球拉到使细线水平的位置A，然后将小球由静止释放，小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零．以下说法正确的是（ ）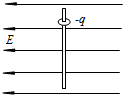
如图所示，在水平向左、电场强度为E的匀强电场中，竖直固定着一根足够长的粗糙绝缘杆，杆上套着一个质量为m、带有电荷量-q的小圆环，圆环与杆间的动摩擦因数为μ．