Question

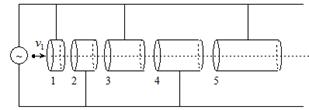
如图所示是一直线加速器原理的示意图，由Ｋ个长度逐个增大的共轴金属圆筒排列成一串（图中只画了5个作为示意），奇数筒和偶数筒分别连接到频率为f、最大电压值为Ｕ的正弦交流电源的两极（设圆筒内部没有电场），整个装置放在真空容器中，圆筒的两底面中心开有小孔。带电粒子从粒子源出发后，经过第一次加速，然后进入第一个圆筒，再向前运动。相邻两圆筒间的间隙很小，问：

　　 比荷为质子（），以沿轴线射入第一个圆筒，此时第1、2两个圆筒间的电势差为。（不计粒子的重力，不计粒子在两圆筒间运动的时间，不考虑相对论效应）

(1).要使质子每次在圆筒间都能获得最大的加速，质子穿越每个圆筒的时间最短为多大？

(2).在(1)的情形下，第n个圆筒的长度应为多大？若质子某次加速后动能为，则下一个圆筒长为多少？( )

(3).若利用回旋加速器使质子最终加速到动能为，则D形盒的半径应为多大？（D形盒中磁感应强度）

Answer 1

解：(1) 　　　　　　　　　　　　　　　　　　　　　（４分）

(2)进入第n个圆筒的速度为，由动能定理：

  　　解得：　　　　　　　（６分）

若：动能　

　　　则　

　　　则　　　　　　　　　　　　　　　　　　　（４分）

(3)质子在回旋加速器中达最大速度时，质子做圆周运动的半径等于D形盒的半径R

　　　　　　    解得：　　　　　（４分）