题目内容
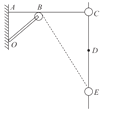
【题目】如图所示,![]() 为一弹性轻绳,一端固定于
为一弹性轻绳,一端固定于![]() 点,一端连接质量为
点,一端连接质量为![]() 的小球,小球穿在竖直的杆上。轻杆
的小球,小球穿在竖直的杆上。轻杆![]() 一端固定在墙上,一端为定滑轮。若绳自然长度等于
一端固定在墙上,一端为定滑轮。若绳自然长度等于![]() ,初始时
,初始时![]() 在一条水平线上,小球从
在一条水平线上,小球从![]() 点由静止释放滑到
点由静止释放滑到![]() 点时速度恰好为零。已知
点时速度恰好为零。已知![]() 、
、![]() 两点间距离为
两点间距离为![]() ,
,![]() 为
为![]() 的中点,小球在
的中点,小球在![]() 点时弹性绳的拉力为
点时弹性绳的拉力为![]() ,小球与杆之间的动摩擦因数为0.5,弹性绳始终处在弹性限度内。下列说法正确的是( )
,小球与杆之间的动摩擦因数为0.5,弹性绳始终处在弹性限度内。下列说法正确的是( )
A.小球在![]() 点时速度最大
点时速度最大
B.若在![]() 点给小球一个向上的速度
点给小球一个向上的速度![]() ,小球恰好能回到
,小球恰好能回到![]() 点,则
点,则![]()
C.小球在![]() 阶段损失的机械能等于小球在
阶段损失的机械能等于小球在![]() 阶段损失的机械能
阶段损失的机械能
D.若![]() 点没有固定,杆
点没有固定,杆![]() 在绳的作用下以
在绳的作用下以![]() 为轴转动,在绳与
为轴转动,在绳与![]() 点分离之前,
点分离之前,![]() 的线速度等于小球的速度沿绳方向分量
的线速度等于小球的速度沿绳方向分量
【答案】AD
【解析】
A.设当小球运动到某点![]() 时,弹性绳的伸长量是
时,弹性绳的伸长量是![]() ,小球受到如图所示的四个力作用:
,小球受到如图所示的四个力作用:

其中
![]()
将![]() 正交分解,则
正交分解,则
![]()
![]()
![]() 的竖直分量
的竖直分量
![]()
据牛顿第二定律得
![]()
解得
![]()
即小球的加速度先随下降的距离增大而减小到零,再随下降的距离增大而反向增大,据运动的对称性(竖直方向可以看作单程的弹簧振子模型)可知,小球运动到![]() 的中点
的中点![]() 时,加速度为零,速度最大,A正确;
时,加速度为零,速度最大,A正确;
B.对小球从![]() 运动到
运动到![]() 的过程,应用动能定理得
的过程,应用动能定理得
![]()
若在![]() 点给小球一个向上的速度
点给小球一个向上的速度![]() ,小球恰能从
,小球恰能从![]() 点回到
点回到![]() 点,应用动能定理得
点,应用动能定理得
![]()
联立解得
![]() ,
,![]()
B错误;
C.除重力之外的合力做功等于小球机械能的变化,小球在![]() 段所受绳子拉力竖直分量较小,则小球在
段所受绳子拉力竖直分量较小,则小球在![]() 段时摩擦力和弹力做的负功比小球在
段时摩擦力和弹力做的负功比小球在![]() 段时摩擦力和弹力做的负功少,小球在
段时摩擦力和弹力做的负功少,小球在![]() 阶段损失的机械能小于小球在
阶段损失的机械能小于小球在![]() 阶段损失的机械能,C错误;
阶段损失的机械能,C错误;
D.绳与![]() 点分离之前
点分离之前![]() 点做圆周运动,线速度(始终垂直于杆)大小等于小球的速度沿绳方向的分量,D正确。
点做圆周运动,线速度(始终垂直于杆)大小等于小球的速度沿绳方向的分量,D正确。
故选AD。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目