题目内容
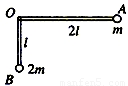 一质量不计的直角形支架两端分别连接质量为m和2m的小球A和 B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内转动,如图所示.开始时OA边处于水平位置,由静止释放,不计任何阻力.转动中设OA边与水平方向的夹角为θ,则当A球速度达最大时θ为 ;假定支架未转动时两小球的总重力势能为Eo,转动中当A的速度为 时两小球的总重力势能为Eo/3.
一质量不计的直角形支架两端分别连接质量为m和2m的小球A和 B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内转动,如图所示.开始时OA边处于水平位置,由静止释放,不计任何阻力.转动中设OA边与水平方向的夹角为θ,则当A球速度达最大时θ为 ;假定支架未转动时两小球的总重力势能为Eo,转动中当A的速度为 时两小球的总重力势能为Eo/3.
【答案】分析:当两个小球系统的质量中心最低时速度最大;也可以用解析法,先假设转过θ,根据系统机械能守恒,列式求出速度的一般表达式,然后再对表达式进行讨论即可.
解答:解:根据题意知,A、B两球的角速度相等,线速度之比等于转动半径之比,为2:1,小球A、B系统中,只有重力势能和动能相互转化,系统机械能守恒,假设转动θ,则OA杆与水平方向的夹角为θ,则A球减小的机械能等于B球增加的机械能,有
mg?2l?sinθ-2mg?(l-lcosθ)=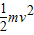 +
+ ?2m
?2m
解得
v=
由数学知识知,当θ=45°时,sinθ+cosθ有最大值,故当θ=45°时,A球的速度最大;
重力势能减小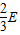 ,故动能增加
,故动能增加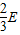 ,有
,有
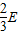 =
= +
+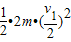
解得
v1=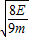
故答案为:45°,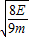 .
.
点评:本题关键根据两个球系统机械能守恒,运用系统机械能守恒定律列式得出速度与转动角度θ之间的关系,然后根据速度表达式进行讨论.
解答:解:根据题意知,A、B两球的角速度相等,线速度之比等于转动半径之比,为2:1,小球A、B系统中,只有重力势能和动能相互转化,系统机械能守恒,假设转动θ,则OA杆与水平方向的夹角为θ,则A球减小的机械能等于B球增加的机械能,有
mg?2l?sinθ-2mg?(l-lcosθ)=
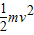 +
+ ?2m
?2m
解得
v=

由数学知识知,当θ=45°时,sinθ+cosθ有最大值,故当θ=45°时,A球的速度最大;
重力势能减小
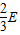 ,故动能增加
,故动能增加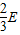 ,有
,有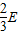 =
= +
+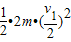
解得
v1=
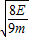
故答案为:45°,
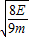 .
.点评:本题关键根据两个球系统机械能守恒,运用系统机械能守恒定律列式得出速度与转动角度θ之间的关系,然后根据速度表达式进行讨论.

练习册系列答案
相关题目
 (2003?上海)一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
(2003?上海)一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( ) 一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( ) (2011?长宁区一模)一质量不计的直角形支架两端分别连接质量为m和2m的小球A和 B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内转动,如图所示.开始时OA边处于水平位置,由静止释放,不计任何阻力.转动中设OA边与水平方向的夹角为θ,则当A球速度达最大时θ为
(2011?长宁区一模)一质量不计的直角形支架两端分别连接质量为m和2m的小球A和 B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内转动,如图所示.开始时OA边处于水平位置,由静止释放,不计任何阻力.转动中设OA边与水平方向的夹角为θ,则当A球速度达最大时θ为 (2007?湖南模拟)一质量不计的直角形支架两端分别连接质量均为m的小球A和B.支架的两直角边长度分别为l和2l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
(2007?湖南模拟)一质量不计的直角形支架两端分别连接质量均为m的小球A和B.支架的两直角边长度分别为l和2l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )