题目内容
如图所示，在 xy 坐标系的第一象项中的一个矩形区域里，存在着沿y轴正方向的匀强电场，该区域的水平宽度为L，竖直宽度足够大．一电子从y轴上的A点（纵坐标为h）以初速v0沿x轴正方向射出，为使电子通过x轴上的B点（横坐标为D），电场强度至少要多大？已知电子的质量为m．电量为e，且L＜D．分析：先画出粒子的运动轨迹图，根据几何关系列式，并根据牛顿运动定律和类平抛运动的规律列式，联立各式表示出电场强度的大小，分析x的大小变化进而得到场强的最小值．
解答：解：设电场的右边界到B的距离为x，在电场中偏转位移为y，偏转角度为θ，其运动轨迹图如右图
，
由几何关系知h=y+xtanθ
其中y=
at2
L=v0t
a=
tanθ=
则h=
(
)2+x
解得E=
；
当电场与y轴重合时，x最大，x=D-L
Emin=
答：电场强度至少要
．
，由几何关系知h=y+xtanθ
其中y=
| 1 |
| 2 |
L=v0t
a=
| Ee |
| m |
tanθ=
| at |
| v0 |
则h=
| 1 |
| 2 |
| eE |
| m |
| L |
| v0 |
| eEL |
| mv20 |
解得E=
2m
| ||
| eL2+2eLx |
当电场与y轴重合时，x最大，x=D-L
Emin=
2m
| ||
| 2edL-eL2 |
答：电场强度至少要
2m
| ||
| 2edL-eL2 |
点评：此题考查带电粒子的偏转，关键画出运动轨迹图，找到各边之间的关系．
练习册系列答案
全能测控期末小状元系列答案
相关题目
如图所示，在 xy坐标系中的一个矩形区域里，存在着沿y轴负方向的匀强电场，场强E=1.0×102N/C，该区域的水平宽度为L=3.0m，竖直宽度足够大．一带电粒子从y轴上的A点（纵坐标为h=2.0m）以初动能Ek=1.0×10-8J沿x轴正方向射出，粒子的带电量为q=1.0×10-10C，为使粒子通过x轴上的B点（横坐标为d=4.0m），则该电场区域应处于何位置，求出其左边界位置对应的横坐标？（不计粒子的重力作用）
（2005?南通模拟）如图所示，在xy平面内有一沿x轴正方向传播的简谐横波，波速为1m/s，振幅为4cm，频率为2.5Hz．在t=0时刻，P点位于其平衡位置上方最大位移处，则距P为0.2m的Q点（ ）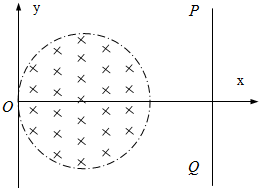
如图所示，在xy平面内有一个半径为R圆形匀强磁场区域，与y轴相切于坐标原点O，磁场强度为B，方向垂直纸面向里，在x=3R处有一个与x轴垂直的荧光屏PQ，t=0时刻，在纸面内从坐标原点O以相等速率向磁场内沿不同的方向发射粒子，粒子的质量为m、电荷量为+q，其中沿x正方向发射的粒子从圆形磁场区域射出时与x轴正方向夹角为60°，粒子的重力不计．