��Ŀ����
14�� �϶�һ�ŵĽ������϶��������Ԥ�ƽ���2011��ǰ���䣬�价�·��еĸ߶Ⱦ����������100km����̽����й���������ݽ��Ȼ��·��и߶�Ϊ200km���϶�һ�Ÿ�����ʵ�����������ǻ������о�����Ϊ����Բ���˶������й����ͼ��ʾ��������
�϶�һ�ŵĽ������϶��������Ԥ�ƽ���2011��ǰ���䣬�价�·��еĸ߶Ⱦ����������100km����̽����й���������ݽ��Ȼ��·��и߶�Ϊ200km���϶�һ�Ÿ�����ʵ�����������ǻ������о�����Ϊ����Բ���˶������й����ͼ��ʾ��������| A�� | �϶���Ż������е����ڱ��϶�һ�ų� | |
| B�� | �϶���Ż������е����ٶȱ��϶�һ�Ŵ� | |
| C�� | �϶���Ż������еĽ��ٶȱ��϶�һ��С | |
| D�� | �϶���Ż�������ʱ���ļ��ٶȱ��϶�һ��С |
���� ����������϶����ǵ����������ṩ���������ɷֱ�õ����ڡ����ٶȡ����ٶȡ����ļ��ٶ������뾶�Ĺ�ϵ��������
��� �⣺�����������ΪM���϶����ǵ�����Ϊm������뾶Ϊr��
����������϶����ǵ����������ṩ��������
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=m$\frac{{4��}^{2}r}{{T}^{2}}$=ma=m��2r
A��T=2��$\sqrt{\frac{{r}^{3}}{GM}}$���϶���Ż������е��߹���뾶���϶�һ��С�������϶���Ż������е����ڱ��϶�һ�Ỵ̂���A����
B��v=$\sqrt{\frac{GM}{r}}$���϶���Ż������е��߹���뾶���϶�һ��С�������϶���Ż������е����ٶȱ��϶�һ�Ŵ�B��ȷ��
C����=$\sqrt{\frac{GM}{{r}^{3}}}$���϶���Ż������е��߹���뾶���϶�һ��С�������϶���Ż������еĽ��ٶȱ��϶�һ�Ŵ�C����
D��a=$\frac{GM}{{r}^{2}}$���϶���Ż������е��߹���뾶���϶�һ��С�������϶���Ż�������ʱ���ļ��ٶȱ��϶�һ�Ŵ�D����
��ѡ��B��
���� ���⿼��������������������Բ���˶�֪ʶ���ʵ�������������Ҫ���ѡ��ʽ����ʽ��

��ϰ��ϵ�д�
 ��������������������ϵ�д�
��������������������ϵ�д�
�����Ŀ
5�� ��ͼ��ʾ������EF�·����������������ǿ�糡����ǿ�ų���һ���������Ӿ���EF��h��ij���ɾ�ֹ��ʼ�����������˶�����A����볡����ǡ��������Բ���˶���Ȼ���B�������CΪԲ������͵㣬����˵������ȷ���ǣ�������
��ͼ��ʾ������EF�·����������������ǿ�糡����ǿ�ų���һ���������Ӿ���EF��h��ij���ɾ�ֹ��ʼ�����������˶�����A����볡����ǡ��������Բ���˶���Ȼ���B�������CΪԲ������͵㣬����˵������ȷ���ǣ�������
 ��ͼ��ʾ������EF�·����������������ǿ�糡����ǿ�ų���һ���������Ӿ���EF��h��ij���ɾ�ֹ��ʼ�����������˶�����A����볡����ǡ��������Բ���˶���Ȼ���B�������CΪԲ������͵㣬����˵������ȷ���ǣ�������
��ͼ��ʾ������EF�·����������������ǿ�糡����ǿ�ų���һ���������Ӿ���EF��h��ij���ɾ�ֹ��ʼ�����������˶�����A����볡����ǡ��������Բ���˶���Ȼ���B�������CΪԲ������͵㣬����˵������ȷ���ǣ�������| A�� | ��B����������ܹ��ٴλص�A�� | |
| B�� | �����ʹh�������A����볡������������Բ���˶� | |
| C�� | �����ʹ���ĵ�����������ӱ�����������ԭ���Ĺ켣�˶� | |
| D�� | ������ȥ�糡E��������켣��͵�ʱ�ܵ�����������һ�������������� |
9��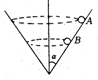 ��ͼ��ʾ�����õĹ⻬Բ���ڲ࣬��������ͬ������С��A��B������ˮƽ����������Բ���˶������й���A��B����Ľ��ٶȡ����ٶȺ����ļ��ٶȵ�˵���У���ȷ���ǣ�������
��ͼ��ʾ�����õĹ⻬Բ���ڲ࣬��������ͬ������С��A��B������ˮƽ����������Բ���˶������й���A��B����Ľ��ٶȡ����ٶȺ����ļ��ٶȵ�˵���У���ȷ���ǣ�������
 ��ͼ��ʾ�����õĹ⻬Բ���ڲ࣬��������ͬ������С��A��B������ˮƽ����������Բ���˶������й���A��B����Ľ��ٶȡ����ٶȺ����ļ��ٶȵ�˵���У���ȷ���ǣ�������
��ͼ��ʾ�����õĹ⻬Բ���ڲ࣬��������ͬ������С��A��B������ˮƽ����������Բ���˶������й���A��B����Ľ��ٶȡ����ٶȺ����ļ��ٶȵ�˵���У���ȷ���ǣ�������| A�� | ���ǵĽ��ٶ�A�ı�B��С | |
| B�� | ���ǵ����ٶ�vA��vB | |
| C�� | ���ǵ����ļ��ٶ���� | |
| D�� | A������ļ��ٶȴ���B������ļ��ٶ� |
3�� һ���ֲ����Ϊ53���б��̶��������̲����Ƶ����ڣ��Ӵ����Ħ������Ϊ0.5����ͼ��ʾ����һ����Ϊ1kg�������ɾ�ֹ��б�涥����б�滬�£��������»������У����̲�����ʼ�վ�ֹ�����У���ȡg=10m/s2����������
һ���ֲ����Ϊ53���б��̶��������̲����Ƶ����ڣ��Ӵ����Ħ������Ϊ0.5����ͼ��ʾ����һ����Ϊ1kg�������ɾ�ֹ��б�涥����б�滬�£��������»������У����̲�����ʼ�վ�ֹ�����У���ȡg=10m/s2����������
 һ���ֲ����Ϊ53���б��̶��������̲����Ƶ����ڣ��Ӵ����Ħ������Ϊ0.5����ͼ��ʾ����һ����Ϊ1kg�������ɾ�ֹ��б�涥����б�滬�£��������»������У����̲�����ʼ�վ�ֹ�����У���ȡg=10m/s2����������
һ���ֲ����Ϊ53���б��̶��������̲����Ƶ����ڣ��Ӵ����Ħ������Ϊ0.5����ͼ��ʾ����һ����Ϊ1kg�������ɾ�ֹ��б�涥����б�滬�£��������»������У����̲�����ʼ�վ�ֹ�����У���ȡg=10m/s2����������| A�� | �����ƵĶ�����10N | |
| B�� | �����ƵĶ�����û�з�����ǰ���������6N | |
| C�� | �����ƶԵ����������Ħ���� | |
| D�� | ��б��ֲ�ʱ�����»������в����Ƶ�ʾ��ΪF1��б��⻬ʱ�����»������в�����ʾ��F2����F1��F2 |
 ��ͼ��ʾ����һ���̶��ĺ�������һ������Ϊm=1kg�Ļ��飬������Ӽ�Ķ�Ħ������Ϊ��=0.5����ʼ�����ں��������Գ��ٶ�v0=2m/s�����˶��������������ײ���ɴκ��ٶȼ�Ϊ�㣬�����ӳ�ΪL=0.1m��������б���ײ��û��������ʧ��������������������������ײ�Ĵ�������g=10m/s2��
��ͼ��ʾ����һ���̶��ĺ�������һ������Ϊm=1kg�Ļ��飬������Ӽ�Ķ�Ħ������Ϊ��=0.5����ʼ�����ں��������Գ��ٶ�v0=2m/s�����˶��������������ײ���ɴκ��ٶȼ�Ϊ�㣬�����ӳ�ΪL=0.1m��������б���ײ��û��������ʧ��������������������������ײ�Ĵ�������g=10m/s2��
 Ϊ�˲ⶨ��ѹ��Vx�����裬��������ͼ1��ʾ�ĵ�·�����У�Vx�Ǵ����ѹ��������3V������Լ3k����V�DZ���ѹ��������2V������Լ2k����R1�ǵ����䣬��ֵ��Χ��0-9999.9����R2�ǻ�����������R3�DZ������裻E�ǵ���飬�綯��6V�����費�ƣ�S1�ǵ����������أ�S2�ǵ���˫�����أ�
Ϊ�˲ⶨ��ѹ��Vx�����裬��������ͼ1��ʾ�ĵ�·�����У�Vx�Ǵ����ѹ��������3V������Լ3k����V�DZ���ѹ��������2V������Լ2k����R1�ǵ����䣬��ֵ��Χ��0-9999.9����R2�ǻ�����������R3�DZ������裻E�ǵ���飬�綯��6V�����費�ƣ�S1�ǵ����������أ�S2�ǵ���˫�����أ� ������Ȧabcd�ij�ab=20cm����bc=10cm������n=100�ѣ���Ȧ�ܵ���R=20����������Ȧλ�ڴ�ֱ����Ȧƽ�����ǿ�ų��ڣ������־�ֹ������ǿ�ų��ĴŸ�Ӧǿ��B��ʱ��t�ı仯��ͼ��ʾ������Ȧ�ĸ�Ӧ�綯��E��t=0.60sʱ��Ȧ��ab�����ܵİ�������С��
������Ȧabcd�ij�ab=20cm����bc=10cm������n=100�ѣ���Ȧ�ܵ���R=20����������Ȧλ�ڴ�ֱ����Ȧƽ�����ǿ�ų��ڣ������־�ֹ������ǿ�ų��ĴŸ�Ӧǿ��B��ʱ��t�ı仯��ͼ��ʾ������Ȧ�ĸ�Ӧ�綯��E��t=0.60sʱ��Ȧ��ab�����ܵİ�������С�� ��ͼ��ʾ��һ����ΪL=0.4m��ֱ���߷���ˮƽ�������ǿ�ų��У�����ˮƽ����ų�����ֱ��������ͨ�����ҵĵ�����
��ͼ��ʾ��һ����ΪL=0.4m��ֱ���߷���ˮƽ�������ǿ�ų��У�����ˮƽ����ų�����ֱ��������ͨ�����ҵĵ�����