题目内容
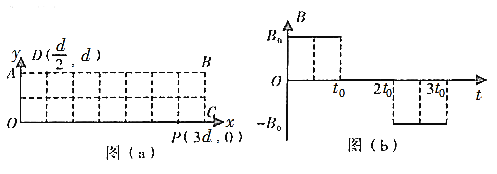
【题目】如图（a），平面直角坐标系xOy的第一象限有长3.5d、宽d的矩形区域OABC，在该区域内施加如图（b）所示的磁场（图中B0和t0未知），假设垂直纸面向里为磁场正方向。若t=0时刻，一比荷为k的电子，从O点以速度
沿y轴正方向射入磁场，则该电子将在0<t<t0的某个时刻从D（
，d）点离开磁场。若t=0时刻，该电子从O点以速度
沿y轴正方向射入磁场，则该电子将在t0<t<2t0的某个时刻从P（3d，0）点离开磁场。求：图（b）中B0和t0的大小？
【答案】
，
【解析】
设电子质量为m、电量为e，则
以
速度射入磁场时，设运行的轨道半径为r，则由
由几何关系
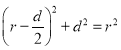
联立求得
若以
的速度射入磁场，设运行的轨道半径为R。则由
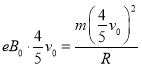
联立解得
设在t0时间内电子在磁场中转过的圆心角为
，在t0时间后电子做直线运动，运动轨迹如图所示
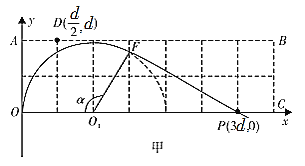
依题意，三角形PFO1是直角三角形，则
所以
可知
设电子在磁场中运动的周期为T，则
又
联立解得
练习册系列答案
相关题目
