题目内容

[探究]一根长为L的均匀细杆可以绕通过其一端的水平轴O在竖直平面内转动，杆最初处于水平位置，杆上距O为a处放有小物体(可视为质点)，杆与其上小物体最初均处于静止状态，如图所示，若此杆突然以角速度ω绕O轴转动，问当ω取什么值时，小物体与杆可能相碰？

答案：
解析：

　　[案例]物体相遇的条件是在相同的时间内物体的路程或位移相等．本题中是物体自由下落的位移与由于杆的转动而引起的相同时间内的杆的两位置与B所在竖直线交点间的距离相等，从图(a)中看出，此最大距离为BD长，即atanθ1．物体做自由落体运动，起始速度较小，速度逐渐变大．而杆在匀速转动，在相同时间内，BC大于自由落体高度，当两者相等时则相遇，相遇的最大距离为BD，即为ω的最大值．若ω再增大时，当物体落至D点时，杆已转过OD位置．则此时不可能相碰，但当ω再增大时，即在物体没有到达D之前杆可能再次转入∠AOD区域．这种情况物体与杆也能相碰，这种情况相遇的最长时间是在D点相遇，此时的ω为这种情况的最小值，只要ω大于该值均能在∠AOD区域内相碰，如图(b)．

　　


练习册系列答案
相关题目
（1）某同学用如图1所示装置探究小车的加速度与力、质量的关系，实验中，他把钩码重力当作小车受到的合力．①为减小把钩码的重力当作小车受到的合力而带来的误差，实验中，除了拉小车的细线与长木板平行外．①还应采取的措施有：
 
 
．（填两条）
②木块从静止开 始运动，利用打点计时器在纸带上记录木块的运动情况，如图2所示，其中O点为纸带上记录到的第一点．A、B、C是该同学在纸带上所取的一些点，下图所标明的数据为A、B、C各点到O点的距离，已知打点计时器所用交流电源频率f=50Hz，木块运动的加速度a=
 
m/s2．（计算结果保留两位有效数字）
精英家教网
（2）有一根长陶瓷管，其表面均匀地镀有一层很薄的电阻膜，管的两端有导电箍M和N，如图3所示．用多用表电阻档测得MN间的电阻膜的电阻约为100Ω，陶瓷管的直径远大于电阻膜的厚度．某同学利用下列器材设计了一个测量该电阻膜厚度d的实验．
A．刻度尺（最小分度为mm）；  B．游标卡尺；
C．电流表A1（量程0～300mA，内阻约0.2Ω）；
D．电流表A2 （量程0～100mA，内阻约0.6Ω）；
E．电压表V1 （量程10V，内阻约5kΩ）；
F．电压表V2 （量程5V，内阻约3kΩ）；
G．滑动变阻器R1 （阻值范围0～30Ω，额定电流1.5A）；
H．滑动变阻器R2 （阻值范围0～1.5KΩ，额定电流1A）；
I．电源E （电动势9V，内阻可不计）；     J．开关一个，导线若干．
①他用毫米刻度尺测出电阻膜的长度为l，用游标卡尺测量该陶瓷管的外径D．
②为了比较准确地测量电阻膜的电阻，且调节方便，实验中应选用电流表
 
，电压表
 
，滑动变阻器
 
．（填写器材前面的字母代号）
③在答题卷方框内画出测量电阻膜的电阻R的实验电路图．
④若电压表的读数为U，电流表的读数为I，镀膜材料的电阻率为ρ，计算电阻膜厚度d （d远小于D）的表达式为：d=
 
（用所测得的量和已知量的符号表示）．

（10分）在“探究单摆摆长与周期关系”的实验中，某同学的主要操作步骤如下：
A．取一根符合实验要求的摆线，下端系一金属小球，上端固定在O点；
B．在小球静止悬挂时测量出O点到小球球心的距离l；
C．拉动小球使细线偏离竖直方向一个不大的角度（约为5°），然后由静止释放小球；
D．用秒表记录小球完成n次全振动所用的时间t。
①用所测物理量的符号表示重力加速度的测量值，其表达式为g=         ；
②若测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是       
（选填下列选项前的序号）
A、测量摆长时，把摆线的长度当成了摆长
B、摆线上端未牢固地固定于O点，振动中出现松动，使摆线越摆越长
C、测量周期时，误将摆球（n-1）次全振动的时间t记为了n次全振动的时间，并由计算式T=t/n求得周期
D、摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后，为了减小实验误差，他决定用图象法处理数据，并通过改变摆长，测得了多组摆长l和对应的周期T，并用这些数据作出T2-l图象如图甲所示。若图线的斜率为k，则重力加速度的测量值g=       。

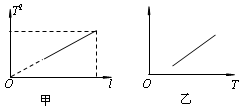
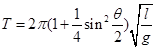④这位同学查阅资料得知，单摆在最大摆角q较大时周期公式可近似表述为。为了用图象法验证单摆周期T和最大摆角q的关系，他测出摆长为l的同一单摆在不同最大摆角q时的周期T，并根据实验数据描绘出如图乙所示的图线。根据周期公式可知，图乙中的纵轴表示的是           ，图线延长后与横轴交点的横坐标为          。

（10分）在“探究单摆摆长与周期关系”的实验中，某同学的主要操作步骤如下：

A．取一根符合实验要求的摆线，下端系一金属小球，上端固定在O点；

B．在小球静止悬挂时测量出O点到小球球心的距离l；

C．拉动小球使细线偏离竖直方向一个不大的角度（约为5°），然后由静止释放小球；

D．用秒表记录小球完成n次全振动所用的时间t。

①用所测物理量的符号表示重力加速度的测量值，其表达式为g=          ；

②若测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是       

（选填下列选项前的序号）

A、测量摆长时，把摆线的长度当成了摆长

B、摆线上端未牢固地固定于O点，振动中出现松动，使摆线越摆越长

C、测量周期时，误将摆球（n-1）次全振动的时间t记为了n次全振动的时间，并由计算式T=t/n求得周期

D、摆球的质量过大

③在与其他同学交流实验方案并纠正了错误后，为了减小实验误差，他决定用图象法处理数据，并通过改变摆长，测得了多组摆长l和对应的周期T，并用这些数据作出T2-l图象如图甲所示。若图线的斜率为k，则重力加速度的测量值g=        。

④这位同学查阅资料得知，单摆在最大摆角q 较大时周期公式可近似表述为。为了用图象法验证单摆周期T和最大摆角q 的关系，他测出摆长为l的同一单摆在不同最大摆角q 时的周期T，并根据实验数据描绘出如图乙所示的图线。根据周期公式可知，图乙中的纵轴表示的是            ，图线延长后与横轴交点的横坐标为           。