题目内容
如图所示，在一次救灾工作中，一架离水面高为H，沿水平直线飞行的直升机A，用悬索(重力可忽略不计)救护困在湖水中的伤员B，已知伤员B的质量为m，不计空气阻力，在直升机A和伤员B以相同的水平速度水平匀速运动的同时，悬索将伤员吊起。A、B之间的距离l随时间t的变化规律为：l =" H" - kt2 (SI制单位，k为给定常数)，则在时间t内伤员的机械能增加了________； t 时刻悬索拉力的瞬时功率为______________。
2mk2t2+mgkt2、2ktm（2k+g）
解析试题分析：飞机t=0时刻离水面高为H，经t时间后，A、B之间的距离为L=H-kt2，故竖直分位移为y=kt2，故初始速度为零，加速度为ay=2k，速度为vy=2kt；所以动能的增加量为：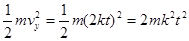
，重力势能的增加量为：mgh=mgkt2；所以机械能的增加量为2mk2t2+mgkt2；设t 时刻悬索拉力为F，则
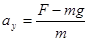，解得F=(2k+g)m，所以t时刻悬索拉力的瞬时功率为2ktm（2k+g）
考点：考查机械能守恒、功率的计算
点评：本题难度较小，本题关键是理清两个分运动，知道机械能增加量等于动能增加量和势能增加量之和，悬索拉力的瞬时功率等于拉力乘以拉力方向上的速度，难度适中
练习册系列答案
相关题目
如图所示，在一次救灾工作中，一架沿水平直线飞行的直升飞机，A用悬索（重力可忽略不计）救护困在湖水中的伤员B．在直升飞机A和伤员B以相同的水平速度匀速运动的同时，悬索将伤员吊起，在某一段时间内，A、B之间的距离以l=H-t2（式中H为直升飞机A离地面的高度，各物理量的单位均为国际单位制单位）规律变化，则在这段时间内（ ）
如图所示，在一次救灾工作中，一架静止在空中的直升机A，用悬索（重力可忽略不计）救起了伤员B．直升机水平方向做初速度为零的匀加速直线运动，竖直方向上伤员与直升飞机的高度差h与时间t的关系为h=H-bt （式中h表示伤员到直升机的竖直距离，H表示开始计时伤员与直升机的高度差，b是一常数，t表示伤员上升的时间）．不计伤员和绳索受到的空气阻力，这段时间内从地面上观察，下面判断正确的是（ ）
如图所示，在一次救灾工作中，一架水平直线飞行的直升飞机A，用悬索救护困在水中的伤员B，在直升飞机A和伤员B以相同的水平速度匀速运动的同时，悬索将伤员吊起，在某一段时间内，A、B之间的距离以l=H-t2（式中H为直升飞机A离水面的高度）规律变化，则在这段时间内（ ）