Question

【题目】如图所示，某星球的半径为R，自转周期为T，a为该星球的近地卫星，b为该星球的同步卫星，其轨道半径为r，已知引力常量为G，则下列说法正确的是

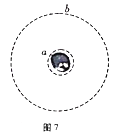
A. a、b两卫星的线速度大小之比为

B. a、b两卫星所受的引力大小之比为

C. 该星球表面的重力加速度为

D. 该星球的平均密度为

Answer 1

【答案】C

【解析】

由万有引力提供向心力可以得到速度和引力大小之比，注意同步卫星的周期等于该星球的自转周期；

A、a、b两卫星与地球之间的万有引力提供向心力，则：，

整理可以得到：，故选项A错误；

B、由题可知a与地球之间的万有引力为：

a与地球之间的万有引力为：

则，故选项B错误；

C、b卫星与地球之间的万有引力提供向心力，则：

忽略地球自转，在地面处重力与万有引力相等，则：

联立可以得到：，故选项C正确；

D、由，可知：，根据密度公式可以得到：

代入可以得到：，故选项D错误。