题目内容
(2011?咸阳三模)如图所示,粒子源产生质量为m,电荷量为+q的粒子(重力不计).粒子从O11孔飘进(初速不计)一个水平方向的加速电场,再经小孔O22进入相互正交的匀强电场和匀强磁场,电场强度大小为E,磁感应强度大小为B11,方向如图,虚线PQ、MN之间存在着方向水平向右的匀强磁场,磁感应强度大小为B22(图中未画出),有一硬质塑料板(不带电,宽度很窄,厚度不计)放置在PQ、MN之间(截面图如图),ab两点恰好分别位于PQ、MN上,且α=450,PQ、MN之间的距离为L,若粒子能沿图中虚线0203进入PQ、MN之间的匀强磁场区域.

(1)求加速电压U;
(2)假设粒子与硬质塑料板相碰后,速度大小不变,方向改变900(即方向改变遵守光的反射定律).求粒子在PQ、MN之间的区域中运动的时间和路程分别是多少?

(1)求加速电压U;
(2)假设粒子与硬质塑料板相碰后,速度大小不变,方向改变900(即方向改变遵守光的反射定律).求粒子在PQ、MN之间的区域中运动的时间和路程分别是多少?
分析:(1)粒子能沿图中虚线0203进入PQ、MN之间的匀强磁场区域,粒子在正交的匀强电场和匀强磁场做匀速直线运动,由电场力与洛伦兹力平衡求出速度,根据动能定理求解加速电压.
(2)粒子从粒子从O3到C做匀速直线运动,与硬质塑料板相碰后,速度方向变为向上,受到洛伦兹力作用,根据左手定则判断得知:从左向右看,粒子逆时针旋转一周后再次与硬质塑料板相碰,相碰后速度方向变为向右,不受洛伦兹力而做匀速直线运动.根据几何知识求出两段匀速直线运动的位移,并求出时间,再由牛顿第二定律求出周期.最后求出总时间.
(2)粒子从粒子从O3到C做匀速直线运动,与硬质塑料板相碰后,速度方向变为向上,受到洛伦兹力作用,根据左手定则判断得知:从左向右看,粒子逆时针旋转一周后再次与硬质塑料板相碰,相碰后速度方向变为向右,不受洛伦兹力而做匀速直线运动.根据几何知识求出两段匀速直线运动的位移,并求出时间,再由牛顿第二定律求出周期.最后求出总时间.
解答:解:(1)由带电粒子在O2O3从沿直线运动有,qv0B1=qE
即 v0=
在加速电场中,由动能定理得,
qU=
mv02
故 U=
(2)带电粒子在PQ、MN之间区域运动轨迹如图所示.

粒子从O3到C和从C到D做匀速直线运动,运动的时间t1和路程s1分别为:
t1=
=
s1=L
粒子与硬质塑料板相碰后,垂直纸面做匀速圆周运动,由匀速圆周运动规律得:
qv0B2=
即 r=
=
T=
粒子做匀速圆周运动的路程s2
S2=2πr=
故粒子在PQ,MN之间的区域中运动的时间t和路程s分别为:
t=t1+T=
+
s=s1+s2=L+
.
答:(1)求加速电压U=
.
(2)粒子在PQ、MN之间的区域中运动的时间和路程分别是
+
,L+
.
即 v0=
| E |
| B1 |
在加速电场中,由动能定理得,
qU=
| 1 |
| 2 |
故 U=
| mE2 | ||
2q
|
(2)带电粒子在PQ、MN之间区域运动轨迹如图所示.

粒子从O3到C和从C到D做匀速直线运动,运动的时间t1和路程s1分别为:
t1=
| L |
| v0 |
| LB1 |
| E |
s1=L
粒子与硬质塑料板相碰后,垂直纸面做匀速圆周运动,由匀速圆周运动规律得:
qv0B2=
m
| ||
| r |
| mv0 |
| qB2 |
| mE |
| qB1B2 |
| 2πm |
| qB2 |
粒子做匀速圆周运动的路程s2
S2=2πr=
| 2πmE |
| qB1B2 |
故粒子在PQ,MN之间的区域中运动的时间t和路程s分别为:
t=t1+T=
| LB1 |
| E |
| 2πm |
| qB2 |
s=s1+s2=L+
| 2πmE |
| qB1B2 |
答:(1)求加速电压U=
| mE2 | ||
2q
|
(2)粒子在PQ、MN之间的区域中运动的时间和路程分别是
| LB1 |
| E |
| 2πm |
| qB2 |
| 2πmE |
| qB1B2 |
点评:本题考查分析和处理粒子在磁场中圆周运动的轨迹问题,要根据几何知识画圆或圆弧.

练习册系列答案
相关题目
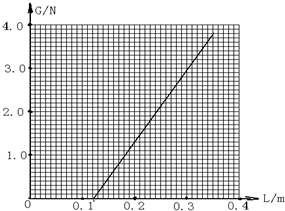 (2011?咸阳三模)某研究小组在“探究弹力和弹簧伸长关系”的实验中,将不同数量的钩碼挂在竖直弹簧下端进行测量,根据实验数据,利用描点法作出钩碼的重力G与弹簧的总长L的关系图象,如图所示
(2011?咸阳三模)某研究小组在“探究弹力和弹簧伸长关系”的实验中,将不同数量的钩碼挂在竖直弹簧下端进行测量,根据实验数据,利用描点法作出钩碼的重力G与弹簧的总长L的关系图象,如图所示 (2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n=
(2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n= (2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )
(2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )