题目内容
质点做初速度为零的匀加速直线运动,由静止开始通过连续三段位移所用时间分别是1s、2s、3s,这三段位移大小之比和这三段位移上的平均速度大小之比分别是( )
| A、1:2:3,1:1:1 | B、1:3:5,1:2:3 | C、12:22:32,12:22:32 | D、13:23:33,12:22:32 |
分析:要求连续的时间不等的三段时间内的位移之比,就要分别求出这三段时间内得位移,要求这三段位移,可以先求第一段的位移,再求前两段的位移,再求前三段的位移,前两段的位移减去第一段的位移,就等于第二段的位移,前三段的位移减去前两段的位移就等于第三段的位移;某段时间内的位移与所用时间的比值就等于该段时间内的平均速度.
解答:解:根据x=
at2可得:
物体通过的第一段位移为:x1=
a×12
又前3s的位移减去前1s的位移就等于第二段的位移
故物体通过的第二段位移为:x2=
a×32-
a×12=
a×8
又前6s的位移减去前3s的位移就等于第三段的位移
故物体通过的第三段位移为:x3=
a×62-
a×32=
a×27
故位移比为:1:8:27=1:23:33
根据平均速度公式:
=
.得:
平均速度之比为:
:
:
=1:4:9
故选:D
| 1 |
| 2 |
物体通过的第一段位移为:x1=
| 1 |
| 2 |
又前3s的位移减去前1s的位移就等于第二段的位移
故物体通过的第二段位移为:x2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又前6s的位移减去前3s的位移就等于第三段的位移
故物体通过的第三段位移为:x3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故位移比为:1:8:27=1:23:33
根据平均速度公式:
. |
| v |
| x |
| t |
平均速度之比为:
| 1 |
| 1 |
| 8 |
| 2 |
| 27 |
| 3 |
故选:D
点评:本题求解第二段和第三段位移的方法十分重要,要注意学习和积累,并能灵活应用

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
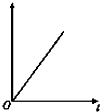 如图所示,是某一质点做直线运动的图象,下列说法中正确的是( )
如图所示,是某一质点做直线运动的图象,下列说法中正确的是( )| A、若纵轴表示速度,横轴表示时间,则质点做匀速直线运动 | B、若纵轴表示位移,横轴表示时间,则质点做匀速直线运动 | C、若纵轴表示速度,横轴表示时间,则质点做初速度为零的匀加速直线运动 | D、若纵轴表示位移,横轴表示时间,则质点做初速度为零的匀加速直线运动 |
 如图所示,是一质点做直线运动的图象,下列说法中正确的是( )
如图所示,是一质点做直线运动的图象,下列说法中正确的是( )