题目内容
 两个等大的弹性球,用两根长为L的细线分别竖直悬挂,静止时两球恰能接触.若把质量较小的球m1拉开使悬线呈水平状态,然后由静止开始释放,相碰后两球升到同样的高度,则两球质量大小有何关系?碰后两球升到多高?
两个等大的弹性球,用两根长为L的细线分别竖直悬挂,静止时两球恰能接触.若把质量较小的球m1拉开使悬线呈水平状态,然后由静止开始释放,相碰后两球升到同样的高度,则两球质量大小有何关系?碰后两球升到多高?分析:m1和m2碰撞过程中,满足动量守恒和机械能守恒列出等式,
m1由静止开始释放到碰撞前过程和相碰后两球升到同样的高度过程机械能守恒列出等式,联立求解.
m1由静止开始释放到碰撞前过程和相碰后两球升到同样的高度过程机械能守恒列出等式,联立求解.
解答:解:设碰撞前m1的速度大小为v1,碰后两球速度大小分别为v′1和v′2,碰后两球上升的高度为h,
在该碰撞过程中,满足动量守恒,规定碰撞前m1的速度方向为正方向,
m1v1=-m1v′1+m2v′2,
根据弹性碰撞规律有:
m1
=
m1
+
m2
m1由静止开始释放到碰撞前过程,根据机械能守恒得:
m1
=m1gL
相碰后两球升到同样的高度,根据机械能守恒得:
m1
=m1gh
m2
=m2gh
联立解得:
m2=3m1,h=
.
答:两球质量大小关系是m2=3m1,碰后两球上升
高度.
在该碰撞过程中,满足动量守恒,规定碰撞前m1的速度方向为正方向,
m1v1=-m1v′1+m2v′2,
根据弹性碰撞规律有:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v′ | 2 1 |
| 1 |
| 2 |
| v′ | 2 2 |
m1由静止开始释放到碰撞前过程,根据机械能守恒得:
| 1 |
| 2 |
| v | 2 1 |
相碰后两球升到同样的高度,根据机械能守恒得:
| 1 |
| 2 |
| v′ | 2 1 |
| 1 |
| 2 |
| v′ | 2 2 |
联立解得:
m2=3m1,h=
| L |
| 4 |
答:两球质量大小关系是m2=3m1,碰后两球上升
| L |
| 4 |
点评:本题综合考查了动量守恒定律、机械能守恒定律综合性较强,关键是理清物体的运动情况,选择合适的规律进行求解.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
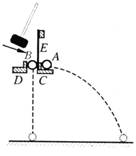
 如图所示为某同学探究物体做平抛运动规律的实验装置,其中A、B为两个等大的小球,C为与弹性钢片E相连的小平台,D为固定支架,两小球等高.用小锤击打弹性钢片E,可使A球沿水平方向飞出,同时B球被松开,做自由落体运动.在不同的高度多次做上述实验,发现两球总是同时落地,这样的实验结果说明
如图所示为某同学探究物体做平抛运动规律的实验装置,其中A、B为两个等大的小球,C为与弹性钢片E相连的小平台,D为固定支架,两小球等高.用小锤击打弹性钢片E,可使A球沿水平方向飞出,同时B球被松开,做自由落体运动.在不同的高度多次做上述实验,发现两球总是同时落地,这样的实验结果说明 (2009?杨浦区模拟)物体做平抛运动的规律可以概括为两点:(1)在水平方向做匀速直线运动;(2)在竖直方向做自由落体运动.图所示为一种研究物体做平抛运动规律的实验装置,其中A、B为两个等大的小球,C为与弹性钢片E相连的小平台,D为固定支架,两小球等高.用小锤击打弹性钢片E,可使A球沿水平方向飞出,同时B球被松开,做自由落体运动.在不同的高度多次做上述实验,发现两球总是同时落地,这样的实验结果:( )
(2009?杨浦区模拟)物体做平抛运动的规律可以概括为两点:(1)在水平方向做匀速直线运动;(2)在竖直方向做自由落体运动.图所示为一种研究物体做平抛运动规律的实验装置,其中A、B为两个等大的小球,C为与弹性钢片E相连的小平台,D为固定支架,两小球等高.用小锤击打弹性钢片E,可使A球沿水平方向飞出,同时B球被松开,做自由落体运动.在不同的高度多次做上述实验,发现两球总是同时落地,这样的实验结果:( )