题目内容
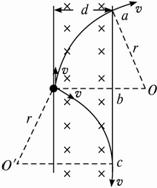
 有一个足够大的匀强电场,场强为E,方向如图所示.一电子以与x轴成45°夹角的初速度v0垂直于电场方向从O点射入.电子质量为m,电荷量为e,不计重力.求:
有一个足够大的匀强电场,场强为E,方向如图所示.一电子以与x轴成45°夹角的初速度v0垂直于电场方向从O点射入.电子质量为m,电荷量为e,不计重力.求:(1)电子通过x轴时的位置;
(2)电子通过x轴时的速度大小.
分析:本题(1)的关键是明确“两坐标轴的方向”,和两分位移的含义,然后再根据类平抛规律即可求解.(2)题的关键是利用平均速度公式求出沿平行于
方向的分速度,然后再求合速度即可.
| v | 0 |
解答:解:(1)电子在电场中做类平抛运动,设电子通过x轴时的位置坐标为(x,0),运动时间为t,则有:
t=xcos4°①
.
=xsin45°②
由式(1)、(2)得:x=
电子通过x轴的位置为x=
.
(2)电子经过x轴时,垂直于电场方向上的速度v0,平行于电场的速度为v1,则有:
.t=xsin45°③
由(1)(3)解得:
=2
,电子经过x轴时的速度V=
=
故电子通过x轴时的速度
.
| v | 0 |
| 1 |
| 2 |
| eE |
| m |
| .t | 2 |
由式(1)、(2)得:x=
2
| ||||
| eE |
电子通过x轴的位置为x=
2
| ||||
| eE |
(2)电子经过x轴时,垂直于电场方向上的速度v0,平行于电场的速度为v1,则有:
0
| ||
| 2 |
由(1)(3)解得:
| v | 1 |
| v | 0 |
|
| 0 |
故电子通过x轴时的速度
| 0 |
点评:遇到类平抛运动时注意对“运动独立性”的理解,然后灵活选取运动学公式求解即可.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

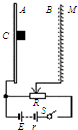 如图所示,在铅板A上有一个放射源C可向各个方向射出速率v为2.04×107 m/s的β射线,B为金属网,A、B连接在电路上,电源电动势E为15V,内阻r为2.5Ω,滑动变阻器在0~10Ω之间可调.图中滑动变阻器滑片置于中点,A、B间距d为10cm,M为荧光屏(足够大),它紧挨着金属网外侧,β粒子穿过金属网打到荧光屏时,荧光屏上就会出现亮斑.已知β粒子的比荷e/m为1.7×1011 C/kg,不计β射线所形成的电流对电路的影响.求:
如图所示,在铅板A上有一个放射源C可向各个方向射出速率v为2.04×107 m/s的β射线,B为金属网,A、B连接在电路上,电源电动势E为15V,内阻r为2.5Ω,滑动变阻器在0~10Ω之间可调.图中滑动变阻器滑片置于中点,A、B间距d为10cm,M为荧光屏(足够大),它紧挨着金属网外侧,β粒子穿过金属网打到荧光屏时,荧光屏上就会出现亮斑.已知β粒子的比荷e/m为1.7×1011 C/kg,不计β射线所形成的电流对电路的影响.求: