题目内容
如图所示,一个半径为R的绝缘光滑半圆环,竖直放在场强为E的匀强电场中,电场方向竖直向下.在环壁边缘处有一质量为m,带有正电荷q的小球,由静止开始下滑,求小球经过最低点时对环底的压力.
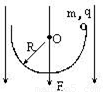
【答案】分析:小球由静止开始下滑的过程中,重力和电场力做功,由动能定理求出小球经过最低点时的速度.小球经过最低点时,由重力、电场力和轨道的支持力的合力提供向心力,由牛顿运动定律求解小球经过最低点时对环底的压力.
解答:解:小球由静止开始下滑的过程中,由动能定理得
mgR+qER=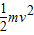 ①
①
小球经过最低点时,由重力、电场力和轨道的支持力的合力提供向心力,则有
N-mg-qE=m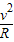 ②
②
联立①②得,轨道对小球的支持力N=3(mg+qE),则由牛顿第三定律知,小球经过最低点时对环底的压力N′=N=3(mg+qE).
答:小球经过最低点时对环底的压力为3(mg+qE).
点评:本题是动能定理和牛顿运动定律结合处理圆周运动中动力学问题,是常用的方法和思路.
解答:解:小球由静止开始下滑的过程中,由动能定理得
mgR+qER=
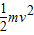 ①
①小球经过最低点时,由重力、电场力和轨道的支持力的合力提供向心力,则有
N-mg-qE=m
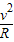 ②
②联立①②得,轨道对小球的支持力N=3(mg+qE),则由牛顿第三定律知,小球经过最低点时对环底的压力N′=N=3(mg+qE).
答:小球经过最低点时对环底的压力为3(mg+qE).
点评:本题是动能定理和牛顿运动定律结合处理圆周运动中动力学问题,是常用的方法和思路.

练习册系列答案
相关题目
 如图所示,一个半径为r、重为G的圆球,被长为r的细绳挂在竖直的光滑的墙壁上,绳与墙所成的角度为30°,则绳子的拉力T和墙壁的弹力N分别是( )
如图所示,一个半径为r、重为G的圆球,被长为r的细绳挂在竖直的光滑的墙壁上,绳与墙所成的角度为30°,则绳子的拉力T和墙壁的弹力N分别是( ) 如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求:
如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求: (2005?浦东新区一模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.
(2005?浦东新区一模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°. (2012?山西二模)如图所示,一个半径为R、质量为M的半圆形光滑小碗,在它的边上
(2012?山西二模)如图所示,一个半径为R、质量为M的半圆形光滑小碗,在它的边上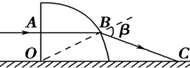 如图所示,一个半径为R的 透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点.已知OA=,该圆柱体对蓝光的折射率为,则:
如图所示,一个半径为R的 透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点.已知OA=,该圆柱体对蓝光的折射率为,则: