题目内容
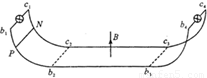
如图所示，两平行的、间距为d的光滑金属导轨b1b2b3b4、c1c2c3c4分别固定在竖直平面内，整个导轨平滑连接，b2b3、c2c3位于同一水平面（规定该水平面的重力势能为零），其间有一边界为b2b3c3c2的、方向竖直向上的匀强磁场，磁感应强度大小为B，导轨两端均连有电阻为R的白炽灯泡．一长为d的金属杆PN与两导轨接触良好，其质量为m、电阻为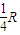
．若金属杆从导轨左侧某一位置开始以初速度υ滑下，通过磁场区域后，再沿导轨右侧上滑至其初始位置高度一半时速度恰为零，此后金属杆做往复运动．金属杆第一次通过磁场区域的过程中，每个灯泡产生的热量为Q，重力加速度为g，除金属杆和灯泡外其余部分的电阻不计．求：（1）金属杆第一次通过磁场区域的过程中损失的机械能．
（2）金属杆初始位置的高度．
（3）金属杆第一次通过磁场区域的过程中加速度的取值范围．
【答案】分析：（1）由于方向竖直向上的匀强磁场位于水平导轨部分，所以金属杆第一次通过磁场区域的过程中损失的机械能具体说是动能转化为回路的电能，而回路的电能最终消耗在两个灯泡和金属杆的电阻上．易错点就是忽视金属杆有电阻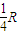
，设通过每一个灯泡的电流有效值I，则回路总电流即通过金属杆的电流有效值为2I，金属杆第一次通过磁场的时间为t，由于每一个灯泡产生的电热Q=I2Rt，则金属杆产生
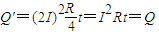，根据能量守恒金属杆第一次通过磁场区域的过程中损失的机械能△E=3Q．
（2）第二小题解决思路是利用金属杆在水平导轨上运动时动能转化为回路的电热．设金属杆第一次进、出磁场的初、末速度为v1、v2，而金属杆的初动能（从下落到进入磁场前金属杆机械能守恒
）、末动能（从出磁场到上升到另一侧最高点
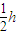金属杆机械能守恒有
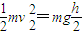）均与初始位置的高度h有关，从而列出一个关于h的方程：
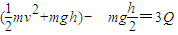求解；
（3）第三小题由金属杆的切割速度v确定动生电动势E=Bdv，金属棒充当电源，内阻为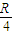
，外电阻是两个灯泡电阻并联
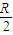，回路总电流I=
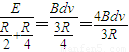通过金属杆，确定安培力大小F安=IdB=
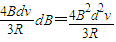，而安培力方向与运动方向向反，所以金属杆做减速运动，安培力随着速度的减少而减小，加速度减小，所以进入金属杆进入磁场时加速度最大，出磁场时加速度最小，由牛顿第二定律确定加速度大小范围，
解答：解：（1）设金属杆第一次通过磁场区域的过程中损失的机械能为△E，
灯泡的并联电阻为：R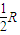1=
①
回路总电阻：R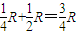2=
②
由焦耳定律，得：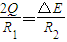
③
由①②③，得：△E=3Q ④
金属杆第一次通过磁场区域的过程中损失的机械能为3Q
（2）设金属杆第一次进、出磁场区域的速度分别为v1，v2，金属杆开始下滑的高度为h，
由能量的转化与守恒定律有：△E=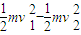
⑤
由机械能守恒定律有：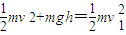
⑥
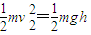⑦
由④⑤⑥⑦，得：h=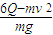
⑧
金属杆初始位置的高度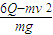
（3）设金属杆第一次进、出磁场区域时的加速度分别为a1，a2，
当金属杆刚进入磁场时产生的电动势为：E1=Bdv1
回流电流：I1=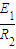
金属杆受到的安培力为F1=BI1d
由牛顿第二定律有：F1=ma1
由②⑥⑧及以上四式，得：a1=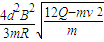
同理可得：a2=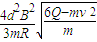
金属杆第一次通过磁场区域的过程中加速度的取值范围：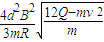
≥a≥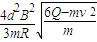
点评：本题的第一小题，易错点是忽视金属杆的电阻产热．对于这类问题，理清解题的思路很重要，本题属于易错题．
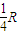，设通过每一个灯泡的电流有效值I，则回路总电流即通过金属杆的电流有效值为2I，金属杆第一次通过磁场的时间为t，由于每一个灯泡产生的电热Q=I2Rt，则金属杆产生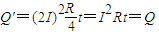，根据能量守恒金属杆第一次通过磁场区域的过程中损失的机械能△E=3Q．（2）第二小题解决思路是利用金属杆在水平导轨上运动时动能转化为回路的电热．设金属杆第一次进、出磁场的初、末速度为v1、v2，而金属杆的初动能（从下落到进入磁场前金属杆机械能守恒
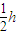）、末动能（从出磁场到上升到另一侧最高点金属杆机械能守恒有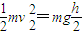）均与初始位置的高度h有关，从而列出一个关于h的方程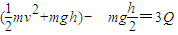：求解；（3）第三小题由金属杆的切割速度v确定动生电动势E=Bdv，金属棒充当电源，内阻为
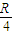，外电阻是两个灯泡电阻并联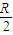，回路总电流I=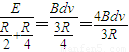通过金属杆，确定安培力大小F安=IdB=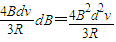，而安培力方向与运动方向向反，所以金属杆做减速运动，安培力随着速度的减少而减小，加速度减小，所以进入金属杆进入磁场时加速度最大，出磁场时加速度最小，由牛顿第二定律确定加速度大小范围，解答：解：（1）设金属杆第一次通过磁场区域的过程中损失的机械能为△E，
灯泡的并联电阻为：R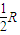1=
①回路总电阻：R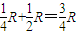2=
②由焦耳定律，得：
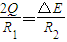③由①②③，得：△E=3Q ④
金属杆第一次通过磁场区域的过程中损失的机械能为3Q
（2）设金属杆第一次进、出磁场区域的速度分别为v1，v2，金属杆开始下滑的高度为h，
由能量的转化与守恒定律有：△E=
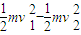⑤由机械能守恒定律有：
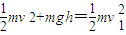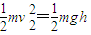⑥ ⑦由④⑤⑥⑦，得：h=
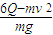⑧金属杆初始位置的高度
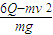
（3）设金属杆第一次进、出磁场区域时的加速度分别为a1，a2，
当金属杆刚进入磁场时产生的电动势为：E1=Bdv1
回流电流：I1=
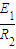
金属杆受到的安培力为F1=BI1d
由牛顿第二定律有：F1=ma1
由②⑥⑧及以上四式，得：a1=
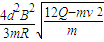
同理可得：a2=
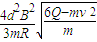
金属杆第一次通过磁场区域的过程中加速度的取值范围：
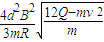≥a≥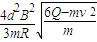点评：本题的第一小题，易错点是忽视金属杆的电阻产热．对于这类问题，理清解题的思路很重要，本题属于易错题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013?常州模拟）如图所示，两平行的虚线间的区域内存在着有界匀强磁场，有一较小的三角形线框abc的ab边与磁场边界平行，现使此线框向右匀速穿过磁场区域，运动过程中始终保持速度方向与ab边垂直．则下列各图中哪一个可以定性地表示线框在进入磁场的过程中感应电流随时间变化的规律（ ）
如图所示，两平行的光滑金属导轨安装在一光滑绝缘斜面上，导轨间距为L，电阻忽略不计且足够长，导轨平面的倾角为α，斜面上相隔为d的平行虚线MN与PQ间有磁感应强度大小为B的匀强磁场，方向与导轨平面垂直．另有一长为2d的绝缘杆将一导体棒和一边长为d（d＜L）的正方形单匝线框连在一起组成一固定的装置，总质量为m，导体棒中通以大小恒为I的电流．将整个装置置于导轨上，线框下边与PQ重合．释放后装置沿斜面开始下滑，当导体棒运动到MN处恰好第一次开始返回，经过若干次往返后，最终整个装置在斜面上作恒定周期的往复运动．导体棒在整个运动过程中始终与导轨垂直．求：
（2009?江苏）如图所示，两平行的光滑金属导轨安装在一光滑绝缘斜面上，导轨间距为l、足够长且电阻忽略不计，导轨平面的倾角为α，条形匀强磁场的宽度为d，磁感应强度大小为B、方向与导轨平面垂直．长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“
”型装置，总质量为m，置于导轨上．导体棒中通以大小恒为I的电流（由外接恒流源产生，图中未画出）．线框的边长为d（d＜l），电阻为R，下边与磁场区域上边界重合．将装置由静止释放，导体棒恰好运动到磁场区域下边界处返回，导体棒在整个运动过程中始终与导轨垂直．重力加速度为g．
（2011?四川模拟）如图所示，两平行的、间距为d的光滑金属导轨b1b2b3b4、c1c2c3c4分别固定在竖直平面内，整个导轨平滑连接，b2b3、c2c3位于同一水平面（规定该水平面的重力势能为零），其间有一边界为b2b3c3c2的、方向竖直向上的匀强磁场，磁感应强度大小为B，导轨两端均连有电阻为R的白炽灯泡．一长为d的金属杆PN与两导轨接触良好，其质量为m、电阻为