题目内容
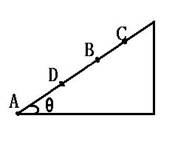 某物体以初动能E0从倾角θ=37°的斜面底A点沿斜面上滑,物体与斜面间的摩擦系数μ=0.5,而且mgsinθ>μmgcosθ。当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E。已知AB=s,求BC的长度。
某物体以初动能E0从倾角θ=37°的斜面底A点沿斜面上滑,物体与斜面间的摩擦系数μ=0.5,而且mgsinθ>μmgcosθ。当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E。已知AB=s,求BC的长度。
(sin37°=0.6、cos37°=0.8)
解:设BC=s`。物体从B点滑到C点再从C点滑到D点的过程中EKB=EKD,即动能的增量为0。在这过程中,重力所做的功与路径无关,它等于mgsinθ•s/2,(3分),摩擦力所做的功为-μmgcosθ(s/2+ 2s`)(3分),由动能定理W合=△EK,(2分)得到:mgsinθ•s/2-μmgcosθ(s/2+ 2s`)=0(3分),s`=(sinθ-μcosθ)s/4μcosθ=s/8(4分)

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
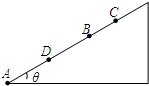 某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )
某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )A、BC段的长度为
| ||
B、BC段的长度为
| ||
C、物体再次返回A点时的动能为
| ||
D、物体再次返回A点时的动能为
|
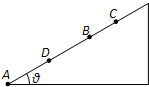 某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )
某物体以初动能E0从倾角θ=37°的斜面底部A点沿斜面上滑,物体与斜面间的动摩擦因数μ=0.5.当物体滑到B点时动能为E,滑到C点时动能为0,物体从C点下滑到AB中点D时动能又为E,则下列说法正确的是(已知|AB|=s,sin37°=0.6,cos37°=0.8)( )
 A.BC段的长度为
A.BC段的长度为