题目内容
如图，半径R=0.8m的光滑圆形轨道固定在竖直面内．小球A、B质量分别为m、3m．A球从左边与圆心等高处由静止开始沿轨道下滑，与静止于轨道最低点的B球相撞，碰撞后A球返回，能达到的最大高度为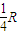
，重力加速度为g，求第一次碰撞刚结束时小球B对轨道的压力．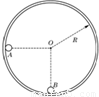
【答案】分析：根据动能定理分别求出A求出与B球碰撞前和碰撞后的速度，结合动量守恒定律求出碰撞后B的速度，从而根据牛顿第二定律求出轨道对B的支持力，得出小球B对轨道的压力．
解答：解：根据动能定理得：
mv12=mgR 得：v1=4m/s
mv1′2=
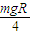得：v1′=2m/s
因为返回，可知v1′与v1反向
根据mv1=m v1′+mv2得：v2=2m/s
设轨道对 B 球的支持力为 N，B 球对轨道的压力为N′．
则N-3mg=3m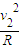
N′=N=4.5mg
方向竖直向下．
答：第一次碰撞刚结束时小球B对轨道的压力为4.5mg，方向竖直向下．
点评：本题综合考查了动能定理、动量守恒定律和牛顿第二定律，综合性较强，关键理清过程，选择合适的规律进行求解．
解答：解：根据动能定理得：
mv12=mgR 得：v1=4m/smv1′2=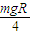 得：v1′=2m/s 因为返回，可知v1′与v1反向
根据mv1=m v1′+mv2得：v2=2m/s
设轨道对 B 球的支持力为 N，B 球对轨道的压力为N′．
则N-3mg=3m
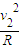
N′=N=4.5mg
方向竖直向下．
答：第一次碰撞刚结束时小球B对轨道的压力为4.5mg，方向竖直向下．
点评：本题综合考查了动能定理、动量守恒定律和牛顿第二定律，综合性较强，关键理清过程，选择合适的规律进行求解．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
（2012?东至县二模）如图，半径R=1.0m的四分之一圆弧形光滑轨道竖直放置，圆弧最低点B与长为L=0.5m的水平面BC相切于B点，BC离地面高h=0.45m，C点与一倾角为θ=37°的光滑斜面连接，质量m=1.0kg的小滑块从圆弧上某点由静止释放，到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍，当小滑块运动到C点时与一个质量M=2.0kg的小球正碰，碰后返回恰好停在B点，已知滑块与水平面间的动摩擦因数?=0.1．（sin37°=0.6 cos37°=0.8，g取l0m/s2）
如图所示，匀强电场方向竖直向上，匀强磁场方向水平且垂直纸面向里，有两个带电小球a和b，a恰能在垂直于磁场方向的竖直平面内做半径r=0.8 m的匀速圆周运动，b恰能以v=2 m/s的水平速度在垂直于磁场方向的竖直平面内向右做匀速直线运动．小球a、b质量ma=10 g，mb=40 g，电荷量qa=1×10-2C，qb=2×10-2C，g=10m/s2．求：
如图，半径R=1.0m的四分之一圆弧形光滑轨道竖直放置，圆弧最低点B与长为L=0.5m的水平面BC相切于B点，BC离地面高h=0.45m，C点与一倾角为θ=37°的光滑斜面连接，质量m=1.0kg的小滑块从圆弧上某点由静止释放，已知滑块与水平面间的动摩擦因数?=0.1．求：
