Question

某行星绕太阳运行的椭圆轨道如图所示，E和F 是椭圆轨道的两个焦点，行星在A点的速度比在B点的速度大，则太阳位于（ ）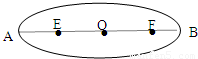

A．F
B．A
C．B
D．E

Answer 1

【答案】分析：开普勒第二定律的内容，对任意一个行星来说，它与太阳的连线在相等时间内扫过相等的面积． 如图所示，行星沿着椭圆轨道运行，太阳位于椭圆的一个焦点上．如果时间间隔相等，即t₂-t₁=t₄-t₃，那么面积A=面积B由此可知行星在远日点B的速率最小，在近日点A的速率最大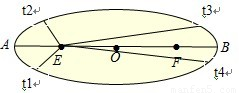
解答：解：根据开普勒第二定律，对任意一个行星来说，它与太阳的连线在相等时间内扫过相等的面积．如果时间间隔相等，即t₂-t₁=t₄-t₃，那么面积A=面积B由此可知，弧长t₁t₂＞弧长t₃t₄则v_A＞V_B即行星在在近日点A的速率最大，远日点B的速率最小，故D正确．
故选D．
点评：考查了开普勒第二定律，再结合时间相等，面积相等，对应弧长求出平均速度．