题目内容
14.已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响.(1)求地球的质量M;
(2)若某一卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求该卫星的运行周期T.
分析 (1)根据万有引力等于重力求出地球的质量.
(2)根据万有引力提供向心力以及万有引力等于重力求出卫星的周期.
解答 解:(1)根据万有引力等于重力得
$\frac{GMm}{{R}^{2}}$=mg
M=$\frac{{gR}^{2}}{G}$,
(2)根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}r}{{T}^{2}}$
r=R+h
M=$\frac{{gR}^{2}}{G}$,
解得:T=2π$\sqrt{\frac{{(R+h)}^{3}}{{gR}^{2}}}$,
答:(1)地球的质量是$\frac{{gR}^{2}}{G}$;
(2)若某一卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,该卫星的运行周期是2π$\sqrt{\frac{{(R+h)}^{3}}{{gR}^{2}}}$.
点评 解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论,并能熟练运用.注意高度h与轨道半径的区别.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图是一簇未标明方向、由单一点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动中只受电场力作用,根据此图不能判断出该带电粒子( )
如图是一簇未标明方向、由单一点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动中只受电场力作用,根据此图不能判断出该带电粒子( )
 如图是一簇未标明方向、由单一点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动中只受电场力作用,根据此图不能判断出该带电粒子( )
如图是一簇未标明方向、由单一点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动中只受电场力作用,根据此图不能判断出该带电粒子( )| A. | 电性与场源电荷的电性相同 | B. | 在a、b两点所受电场力大小Fa>Fb | ||
| C. | 在a、b两点时速度大小va>vb | D. | 在a、b两点的电势能Ea<Eb |
5. 如图所示,在滑动变阻器的滑片向右滑动的过程中,理想电压表、电流表的示数将发生变化,电压表V1、V2示数变化量的绝对值分别为△U1、△U2,已知电阻R大于电源内阻r,则( )
如图所示,在滑动变阻器的滑片向右滑动的过程中,理想电压表、电流表的示数将发生变化,电压表V1、V2示数变化量的绝对值分别为△U1、△U2,已知电阻R大于电源内阻r,则( )
 如图所示,在滑动变阻器的滑片向右滑动的过程中,理想电压表、电流表的示数将发生变化,电压表V1、V2示数变化量的绝对值分别为△U1、△U2,已知电阻R大于电源内阻r,则( )
如图所示,在滑动变阻器的滑片向右滑动的过程中,理想电压表、电流表的示数将发生变化,电压表V1、V2示数变化量的绝对值分别为△U1、△U2,已知电阻R大于电源内阻r,则( )| A. | 电流表A的示数增大 | B. | 电压表V2的示数增大 | ||
| C. | 电压表V1的示数增大 | D. | △U1大于△U2 |
2.关于地球同步卫星下列判断正确的是( )
| A. | 运行速度大于7.9 km/s | |
| B. | 离地面高度一定,相对地面静止 | |
| C. | 绕地球运行的角速度比月球绕地球运行的角速度小 | |
| D. | 向心加速度与静止在赤道上物体的向心加速度大小相等 |
9.关于地球的第一宇宙速度,下列说法不正确的是( )
| A. | 它是人造地球卫星绕地球作匀速圆周运动的最大速度 | |
| B. | 它是人造地球卫星在近地表面圆形轨道上的运行速度 | |
| C. | 它是能使卫星绕地球作匀速圆周运动的最小发射速度 | |
| D. | 它是人造卫星绕地球作椭圆轨道运行时在近地点的速度 |
19.两位同学分别在塔的不同高度,用两个轻重不同的球做自由落体实验,已知甲球重力是乙球的2倍,释放甲球处的高度是释放乙球处高度的$\frac{1}{2}$,则( )
| A. | 甲球落地的时间是乙球的$\frac{1}{2}$ | |
| B. | 甲球落地时的速度是乙球的$\frac{1}{2}$ | |
| C. | 甲乙两球在开始下落1s内的位移比是$\frac{1}{2}$ | |
| D. | 甲、乙两球各落下1m时的速度相等 |
6.质量为M的人在游乐园乘坐过山车时,人随车在竖直平面内做圆周运动,下列说法中正确的是( )
| A. | 人在最高点时处于倒坐状态,如果没有保险带,人一定会掉下来 | |
| B. | 人在最低点时处于失重状态 | |
| C. | 人在最低点对座位的压力一定大于人的重力Mg | |
| D. | 人在最高点时对座位的压力一定小于人的重力Mg |
3.如图是氧气分子在不同温度(0℃和100℃)下的速率分布,由图可得信息( )


| A. | 随着温度的升高,每个氧气分子速率都增大 | |
| B. | 同一温度下,氧气分子速率呈现出“中间多两头少”分布规律 | |
| C. | 随着温度的升高,氧气分子中速率小的分子所占的比例高 | |
| D. | 随着温度的升高,氧气分子的平均速率减小 |
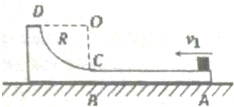 竖直平面内的轨道ABCD由水平滑道AB与半径为R的光滑的四分之一滑道CD组成,AB恰好与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示,一个质量为m=1kg的小物块(可视为质点)从轨道的A端以初速度v1=4m/s冲上水平滑道AB,沿着滑道运动,由DC弧滑下后最终停止在水平滑道AB的中间位置.已知水平滑道AB长为L=1m,轨道ABCD的质量为M=3kg.重力加速度g=10m/s2.求:
竖直平面内的轨道ABCD由水平滑道AB与半径为R的光滑的四分之一滑道CD组成,AB恰好与圆弧CD在C点相切,轨道放在光滑的水平面上,如图所示,一个质量为m=1kg的小物块(可视为质点)从轨道的A端以初速度v1=4m/s冲上水平滑道AB,沿着滑道运动,由DC弧滑下后最终停止在水平滑道AB的中间位置.已知水平滑道AB长为L=1m,轨道ABCD的质量为M=3kg.重力加速度g=10m/s2.求: