题目内容
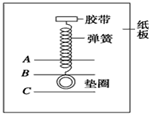（2008?镇江模拟）一个研究性学习小组设计了一个竖直加速度器，如图所示．把轻弹簧上端用胶带固定在一块纸板上，让其自然下垂，在弹簧末端处的纸板上刻上水平线A．现把垫圈用胶带固定在弹簧的下端，在垫圈自由垂下处刻上水平线B，在B的下方刻一水平线C，使AB间距等于BC间距．假定当地重力加速度g=10m/s2，当加速度器在竖直方向运动时，下列说法错误的是（ ）分析：弹簧末端的垫圈在B处时，知弹簧的弹力等于中，根据弹力的大小，运用牛顿第二定律和胡克定律得出加速度的大小和方向，从而判断出加速器的运动情况．
解答：解：A、若弹簧末端的垫圈在A处，弹簧的弹力为零，则对垫圈分析，根据牛顿第二定律得：a=g．方向竖直向下．故A正确．
B、当弹簧末端在垫圈B处时，垫圈所受的合力为零，则整体合力为零，加速度为零．故B错误．
C、当弹簧的末端的垫圈在C处时，根据胡克定律知弹力变为在B处时的2倍，根据牛顿第二定律得：
a=
=g，方向竖直向上．则F-mg=ma，F=mg+ma=2mg=1N．故C正确．
D、若弹簧末端的垫圈在BC之间某处，合力的方向向上，加速度向上，则加速器可能向上做加速运动，也可能向下做减速运动．故D错误．
本题选错误的，故选D．
B、当弹簧末端在垫圈B处时，垫圈所受的合力为零，则整体合力为零，加速度为零．故B错误．
C、当弹簧的末端的垫圈在C处时，根据胡克定律知弹力变为在B处时的2倍，根据牛顿第二定律得：
a=
| 2mg-mg |
| m |
D、若弹簧末端的垫圈在BC之间某处，合力的方向向上，加速度向上，则加速器可能向上做加速运动，也可能向下做减速运动．故D错误．
本题选错误的，故选D．
点评：解决本题的关键知道垫圈与加速器具有相同的加速度，通过对垫圈分析得出整体的加速度大小和方向．
练习册系列答案
相关题目
（2008?镇江模拟）如图所示，质量为m的长方体物块放在水平放置的钢板C上，物块与钢板间的动摩擦因数为μ，由于光滑固定导槽A、B的控制，该物块只能沿水平导槽运动．现使钢板以速度v1向右匀速运动，同时用水平力F拉动物块使其以速度v2（v2的方向与vl的方向垂直，沿y轴正方向）沿槽匀速运动，以下说法正确的是（ ）
（2008?镇江模拟）一个质量为m带电量为+q的小球以水平初速度v0自离地面h高度处做平抛运动．不计空气阻力．重力加速度为g．试回答下列问题：
（2008?镇江模拟）如图所示，两个闭合的金属圆环，穿在一根光滑的绝缘杆上，当条形磁铁自右向左插向圆环时，两圆环的运动是（ ）