题目内容
 如图所示,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力(取sin37°=0.60,cos37°=0.80;g取10m/s2),求:
如图所示,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力(取sin37°=0.60,cos37°=0.80;g取10m/s2),求:(1)A点与O点的距离L;
(2)运动员离开O点时的水平速度大小;
(3)运动员落到A点时的速度.
分析:(1)平抛运动在竖直方向上做自由落体运动,根据时间求出平抛运动的竖直位移,从而求出AO的距离.
(2)根据水平位移和时间求出平抛运动的初速度.
(3)根据竖直方向上的运动规律求出A点竖直方向上的分速度,根据平行四边形定则求出A点的速度.
(2)根据水平位移和时间求出平抛运动的初速度.
(3)根据竖直方向上的运动规律求出A点竖直方向上的分速度,根据平行四边形定则求出A点的速度.
解答:解:(1)根据h=
gt2得,h=
×10×9m=45m.
所以L=
=
m=75m.
(2)水平位移x=Lcos37°=60m.
则平抛运动的初速度v0=
=
m/s=20m/s.
(3)A点竖直方向上的分速度vy=gt=30m/s.
则A点的速度vA=
=10
m/s.
答:(1)A点与O点的距离L为75m.
(2)运动员离开O点时的水平速度大小为20m/s.
(3)运动员落到A点时的速度大小为10
m/s.
| 1 |
| 2 |
| 1 |
| 2 |
所以L=
| h |
| sin37° |
| 45 |
| 0.6 |
(2)水平位移x=Lcos37°=60m.
则平抛运动的初速度v0=
| x |
| t |
| 60 |
| 3 |
(3)A点竖直方向上的分速度vy=gt=30m/s.
则A点的速度vA=
| v02+vy2 |
| 13 |
答:(1)A点与O点的距离L为75m.
(2)运动员离开O点时的水平速度大小为20m/s.
(3)运动员落到A点时的速度大小为10
| 13 |
点评:解决本题的关键知道平抛运动的水平方向和竖直方向上的运动规律,抓住等时性,结合运动学公式进行求解.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
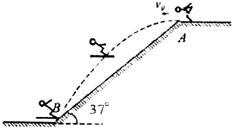 跳台滑雪是一种极为壮观的运动,运动员穿着滑雪板,从跳台水平飞出,在空中飞行一段距离后着陆,如图所示.设运动员连同滑雪板的总质量m=50kg,从倾角θ=37°的坡顶A点以速度v0=20m/s沿水平方向飞出,恰落到山坡底的水平商上的B处.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
跳台滑雪是一种极为壮观的运动,运动员穿着滑雪板,从跳台水平飞出,在空中飞行一段距离后着陆,如图所示.设运动员连同滑雪板的总质量m=50kg,从倾角θ=37°的坡顶A点以速度v0=20m/s沿水平方向飞出,恰落到山坡底的水平商上的B处.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
