题目内容
一辆电动车，蓄电池充满后可向电动机提供E=4.5×106J的能量，已知车辆总质量M=150kg，行驶时所需克服的阻力F阻是车辆总重力的0.05倍．（1）若这辆车的电动机的效率η=80%，则这辆车充一次电能行驶的最大距离是多少？（g取10m/s2）
（2）若电动车蓄电池的电动势E1=24V，工作时的电流强度I=20A，设电动车电路中总电阻为R，蓄电池工作时有20%的能量在R上转化为内能．求R的大小．
【答案】分析：（1）当匀速行驶时，F=F阻，根据电动车克服阻力所做的功等于蓄电池充满后用于行车有效的能量求解．
（2）由能量关系求得在R上转化为内能，再根据焦耳定律求得R的大小．
解答：解：（1）当匀速行驶时，F=F阻，
由题意得电动车克服阻力所做的功等于蓄电池充满后用于行车有效的能量．
ηE=F阻xmax
所以xmax=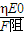
=
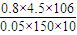m=4.8×104m=48km
（2）蓄电池工作时有20%的能量在R上转化为内能．
由能量关系PR=η′E1I
又因为PR=I2R，
所以R=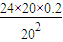
=0.24Ω
答案：（1）这辆车充一次电能行驶的最大距离是48km
（2）R的大小是0.24Ω．
点评：本题考查了电功、电功率的计算和功的计算，解决这类综合性题目要求有扎实的物理功底，还要有提取信息的能力，再具体分析求解．
（2）由能量关系求得在R上转化为内能，再根据焦耳定律求得R的大小．
解答：解：（1）当匀速行驶时，F=F阻，
由题意得电动车克服阻力所做的功等于蓄电池充满后用于行车有效的能量．
ηE=F阻xmax
所以xmax=
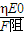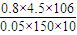=m=4.8×104m=48km（2）蓄电池工作时有20%的能量在R上转化为内能．
由能量关系PR=η′E1I
又因为PR=I2R，
所以R=
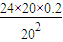=0.24Ω答案：（1）这辆车充一次电能行驶的最大距离是48km
（2）R的大小是0.24Ω．
点评：本题考查了电功、电功率的计算和功的计算，解决这类综合性题目要求有扎实的物理功底，还要有提取信息的能力，再具体分析求解．
练习册系列答案
相关题目