题目内容
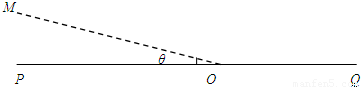
如图所示,在竖直平面内,虚线MO与水平线PQ相交于O,二者夹角θ=30°,在MO左侧存在电场强度为E、方向竖直向下的匀强电场,MO右侧某个区域存在磁感应强度为B、垂直纸面向里的匀强磁场,O点处在磁场的边界上,现有一群质量为m、电量为+q的带电粒子在纸面内以速度v(0≤v≤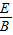 )垂直于MO从O点射入磁场,所有粒子通过直线MO时,速度方向均平行于PQ向左,不计粒子的重力和粒子间的相互作用力.求:
)垂直于MO从O点射入磁场,所有粒子通过直线MO时,速度方向均平行于PQ向左,不计粒子的重力和粒子间的相互作用力.求:(1)速度最大的粒子从O开始射入磁场至返回水平线POQ所用的时间.
(2)磁场区域的最小面积.
【答案】分析:(1)粒子的运动轨迹如图所示,设粒子在匀强磁场中做匀速圆周运动的半径为R,周期为T,先求出粒子在匀强磁场中运动时间,粒子自N点水平飞出磁场,出磁场后应做匀速运动至OM,根据几何关系及速度时间公式求出时间,过MO后粒子做类平抛运动,根据平抛运动的基本公式求出此过程中的时间,三段时间之和即为总时间;
(2)由题知速度大小不同的粒子均要水平通过OM,则其飞出磁场的位置均应在ON的连线上,故磁场范围的最小面积△S是速度最大的粒子在磁场中的轨迹与ON所围成的面积.
解答: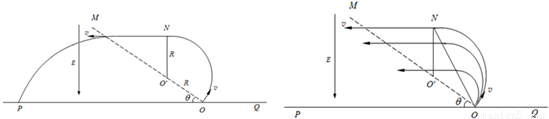 解:(1)粒子的运动轨迹如图所示,设粒子在匀强磁场中做匀速圆周运动的半径为R,周期为T,粒子在匀强磁场中运动时间为t1
解:(1)粒子的运动轨迹如图所示,设粒子在匀强磁场中做匀速圆周运动的半径为R,周期为T,粒子在匀强磁场中运动时间为t1
则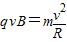
解得:
T=
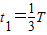
设粒子自N点水平飞出磁场,出磁场后应做匀速运动至OM,设匀速运动的距离为s,匀速运动的时间为t2,由几何关系知:
s=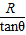
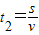
过MO后粒子做类平抛运动,设运动的时间为t3,
则:
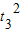
又由题知: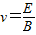
则速度最大的粒子自O进入磁场至重回水平线POQ所用的时间为:
t=t1+t2+t3=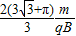
(2)由题知速度大小不同的粒子均要水平通过OM,则其飞出磁场的位置均应在ON的连线上,故磁场范围的最小面积△S是速度最大的粒子在磁场中的轨迹与ON所围成的面积,
扇形OO′N的面积的面积S=
△OO′N的面积为:S′=R2cos30°sin30°=
△S=S-S′
解得:△S=
答:(1)速度最大的粒子从O开始射入磁场至返回水平线POQ所用的时间为 .
.
(2)磁场区域的最小面积为 .
.
点评:做好此类题目的关键是准确的画出粒子运动的轨迹图,利用几何知识求出粒子运动的半径,再结合半径公式和周期公式去分析.
(2)由题知速度大小不同的粒子均要水平通过OM,则其飞出磁场的位置均应在ON的连线上,故磁场范围的最小面积△S是速度最大的粒子在磁场中的轨迹与ON所围成的面积.
解答:
 解:(1)粒子的运动轨迹如图所示,设粒子在匀强磁场中做匀速圆周运动的半径为R,周期为T,粒子在匀强磁场中运动时间为t1
解:(1)粒子的运动轨迹如图所示,设粒子在匀强磁场中做匀速圆周运动的半径为R,周期为T,粒子在匀强磁场中运动时间为t1则
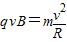
解得:

T=

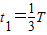
设粒子自N点水平飞出磁场,出磁场后应做匀速运动至OM,设匀速运动的距离为s,匀速运动的时间为t2,由几何关系知:
s=
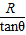
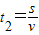
过MO后粒子做类平抛运动,设运动的时间为t3,
则:

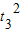
又由题知:
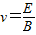
则速度最大的粒子自O进入磁场至重回水平线POQ所用的时间为:
t=t1+t2+t3=
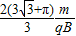
(2)由题知速度大小不同的粒子均要水平通过OM,则其飞出磁场的位置均应在ON的连线上,故磁场范围的最小面积△S是速度最大的粒子在磁场中的轨迹与ON所围成的面积,
扇形OO′N的面积的面积S=

△OO′N的面积为:S′=R2cos30°sin30°=

△S=S-S′
解得:△S=

答:(1)速度最大的粒子从O开始射入磁场至返回水平线POQ所用的时间为
 .
.(2)磁场区域的最小面积为
 .
.点评:做好此类题目的关键是准确的画出粒子运动的轨迹图,利用几何知识求出粒子运动的半径,再结合半径公式和周期公式去分析.

练习册系列答案
相关题目
 (2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( )
(2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( ) 如图所示,在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平初速V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能可能为( )
如图所示,在竖直平面内有一边长为L的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平初速V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能可能为( ) 如图所示,在竖直平面内有一半圆形轨道,圆心为O,一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出,落于圆轨道上的C点,已知OC的连线与OA的夹角为θ,求小球从A到C的时间t=?(空气阻力不计)
如图所示,在竖直平面内有一半圆形轨道,圆心为O,一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出,落于圆轨道上的C点,已知OC的连线与OA的夹角为θ,求小球从A到C的时间t=?(空气阻力不计)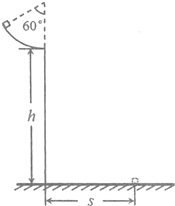 如图所示,在竖直平面内有一个粗糙的
如图所示,在竖直平面内有一个粗糙的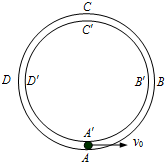 如图所示,在竖直平面内固定两个很靠近的同心圆形轨道,外轨道ABCD光滑,内轨道A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.
如图所示,在竖直平面内固定两个很靠近的同心圆形轨道,外轨道ABCD光滑,内轨道A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑,一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,已知圆形轨道的半径R=0.32m,取g=10m/s2.