题目内容
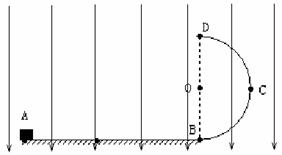
如图所示,可视为质点的物体质量为m=0.4kg、电量为q=+2.0×10-2C,与水平绝缘轨道间的动摩擦因数为µ=0.2,水平轨道与半径为R=0.4m的竖直光滑半圆形绝缘轨道相切于B点,AB间距为L=1.0m,轨道整体固定在地面上,空间内存在竖直向下的匀强电场,场强为E=1.0×102N/C。重力加速度g取10m/s2.物体在半圆形轨道上的B点时对轨道的压力与物体在AB间时对轨道的压力之比,称为物体运动的压力比,则:
(1)若使物体运动的压力比为24,则物体在出发点A的速度应为多大?
(2)若物体在出发点A开始水平向右运动,并沿圆弧轨道由D点飞出,则物体运动的压力比及物体在出发点A的速度应满足什么条件?
(3)若使物体运动的压力比为1.5,则物体运动后停的位置距离出发点A的距离为多少?
(1)对物体由A运动到B的过程,应用动能定理可得:
—μ(mg+qE)L=![]() mvB2-
mvB2-![]() mvA2………………①
mvA2………………①
物体在AB间时对轨道的压力N1=mg+qE………………②
对物体在B点,应用牛顿第二定律可得:N2-(mg+qE)= ![]() ………………③
………………③
设物体运动的压力比为n,则n=![]() =24………………④
=24………………④
由①~④可得:vA=12m/s………………⑤
(2)根据题意,可设对应的D点的速度为VD,
对物体在B点,应用牛顿第二定律可得:mg+qE≤![]() ………………⑥
………………⑥
对物体由B运动到D的过程,应用动能定理可得:— (mg+qE)2R=![]() mvD2-
mvD2-![]() mvB2……………⑦
mvB2……………⑦
对物体由A运动到D的过程,应用动能定理可得:
—μ(mg+qE)L— (mg+qE)2R=![]() mvD2-
mvD2-![]() mvA2………………⑧
mvA2………………⑧
由⑥⑧可得:vA≥6m/s………………⑨
由②③⑦可得:n≥6………………⑩
⑶根据题意可知:n=![]() =1.5………………
=1.5………………![]()
由②③![]() 可得:
可得:![]() (mg+qE)=
(mg+qE)= ![]() ………………
………………![]()
对物体由B沿圆形轨道上滑的过程,由机械能守恒定律可知:![]() mvB2=
mvB2=![]() (mg+qE)R………………
(mg+qE)R………………![]()
即物体只能沿圆形轨道上滑至高度为![]() R处,后又沿原路径滑下,设物体所停位置与B的距离为S,
R处,后又沿原路径滑下,设物体所停位置与B的距离为S,
对物体由B滑出S远的过程,应用动能定理可得:—μ(mg+qE)S= -![]() mvB2………………
mvB2………………![]()
代入数据,可得:S=0.5m………………![]()
物体运动后停的位置与A的距离为L-S=0.5m………………![]()

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )
如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( ) (2013?普陀区一模)如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、
(2013?普陀区一模)如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、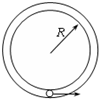 如图所示,可视为质点、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )
如图所示,可视为质点、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( ) 如图所示,可视为质点的小球用细线拉住并放在光滑斜面上,斜面体放在光滑水平面上,水平力F作用在斜面体上使之处于静止.细线的拉力为T,斜面对小球的支持力大小为FN.缓慢向左推动斜面体在小球未脱离斜面的过程中,下列说法中正确的是( )
如图所示,可视为质点的小球用细线拉住并放在光滑斜面上,斜面体放在光滑水平面上,水平力F作用在斜面体上使之处于静止.细线的拉力为T,斜面对小球的支持力大小为FN.缓慢向左推动斜面体在小球未脱离斜面的过程中,下列说法中正确的是( ) (1)一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是:下列描述中正确的是
(1)一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是:下列描述中正确的是