题目内容
据有关资料介绍，受控核聚变装置中有极高的温度，因而带电粒子（核聚变的原料）将没有通常意义上的“容器”可装，而是由磁场来约束带电粒子运动使之束缚在某个区域内，右图是它的截面图，在外径为R2=1.2m、内径R1=0.6m的环状区域内有垂直于截面向里的匀强磁场，磁感强度B=0.4T，若氦核（其比荷q/m=4.8×107c/kg）在平行于截面的平面内从内圆上A点沿各个方向射入磁场都不能穿出磁场的外边界，求氦核的最大速度．（不计带电粒子的重力）
设氦核沿与内圆相切方向射入磁场，且轨道与外圆相切时的速度为vm，则从A点以vm速度沿各方向射入磁场区的氦核都不能穿出磁场外边界，如图所示．由图知
r′=
=0.3m．
由qvB=m
，得r=
，
氦核不穿出磁场外边界应满足的条件是
≤r′，
所以从内圆上A点沿各个方向射入磁场都不能穿出磁场的外边界时，氦核的速度范围为
vm≤
=5.76×106m/s．
答：氦核的最大速度为5.76×106m/s．
r′=
| R2-R1 |
| 2 |
由qvB=m
| v2 |
| r |
| mv |
| qB |
氦核不穿出磁场外边界应满足的条件是
| mvm |
| qB |
所以从内圆上A点沿各个方向射入磁场都不能穿出磁场的外边界时，氦核的速度范围为
vm≤
| Bqr′ |
| m |
答：氦核的最大速度为5.76×106m/s．
练习册系列答案
相关题目
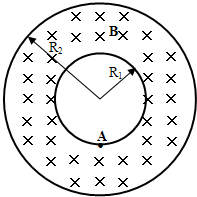据有关资料介绍，受控核聚变装置中有极高的温度，因而带电粒子将没有通常意义上的“容器”可装，而是由磁场约束带电粒子运动使之束缚在某个区域内．现按下面的简化条件来讨论这个问题：如图所示是一个截面为内径R1=0.6m、外径R2=1.2m的环状区域，区域内有垂直于截面向里的匀强磁场．已知氦核的荷质比
据有关资料介绍，受控核聚变装置中有极高的温度，因而带电粒子（核聚变的原料）将没有通常意义上的“容器”可装，而是由磁场来约束带电粒子运动使之束缚在某个区域内，右图是它的截面图，在外径为R2=1.2m、内径R1=0.6m的环状区域内有垂直于截面向里的匀强磁场，磁感强度B=0.4T，若氦核（其比荷q/m=4.8×107c/kg）在平行于截面的平面内从内圆上A点沿各个方向射入磁场都不能穿出磁场的外边界，求氦核的最大速度．（不计带电粒子的重力）
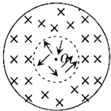据有关资料介绍，受控核聚变装置中有极高的温度，因而带电粒子将没有通常意义上的“容器”可装，而是由磁场约束带电粒子运动使之束缚在某个区域内（托卡马克装置）．如图所示，环状匀强磁场围成中空区域，中空区域中的带电粒子只要速度不是很大，都不会穿出磁场的外边缘而被约束在该区域内，设环状磁场的内半径为R1=0.5m，外半径R2=1.0m，磁场的磁感应强度B=1.0T，若被束缚带电粒子的比荷为
据有关资料介绍，受控热核聚变装置中有极高的温度，因而带电粒子将没有通常意义上的“容器”可装，而是由磁场约束使其在某个区域内运动．现按下面的简化条件来讨论这个问题：如图所示是一个内径R1=1.0m，外径R2=2.0m的环状区域的截面，区域内有垂直截面向里的匀强磁场，O点为氦核源，它能沿半径方向射出各种速率的氦核，已知氦核的比荷
，外半径为R2=1． 0 m，区域内有垂直纸面向里的匀强磁场，已知磁感应强度B=1．0 T，被束缚粒子的荷质比为
=4．0×107C/kg，不计带电粒子在运动过程中的相互作用，不计带电粒子的重力．