Question

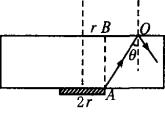
如图所示，在厚度为d、折射率为n的大玻璃板的下表面，紧贴着一个半径为r的圆形发光面，为了从玻璃板的上方看不见圆形发光面，可在玻璃板的上表面贴一张圆形黑纸片．求所贴黑纸片的最小面积．

Answer 1

答案：
解析：

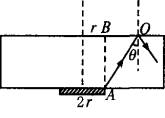
解析：如图所示，A为发光面右边缘，由A发出的光线射向O点恰好发生全反射，入射角q刚好为玻璃的临界角．在O点外侧玻璃的上表面不再有折射光线，B点为A在玻璃正上方的对应点，那么r＋BO为玻璃上表面透光面圆的最大半径．由临界角公式：sinq＝ 由几何关系sinq＝ 解得：OB＝ 所以圆纸片半径R＝r＋ 圆纸片的面积S＝p（r＋）2． 说明：解答本题的关键是弄清所贴纸片的最小面积究竟由什么决定．通过对光线的跟踪分析搞清所贴纸片的最小面积决定于什么，这道题的实质就变成了利用全反射知识求介质的临界角．