题目内容
 小汽车甲以8m/s的速度在平直的公路上向右匀速行驶.某时刻,发现在其正前方20m处,有一货车乙刚好以2m/s2的加速度由静止开始向右做匀加速直线运动,且当乙车速度达到12m/s时,便保持此速度匀速运动,而甲车继续匀速运动.
小汽车甲以8m/s的速度在平直的公路上向右匀速行驶.某时刻,发现在其正前方20m处,有一货车乙刚好以2m/s2的加速度由静止开始向右做匀加速直线运动,且当乙车速度达到12m/s时,便保持此速度匀速运动,而甲车继续匀速运动.(1)求乙车速度增加到8m/s所用的时间
(2)判断甲车能否追上乙车?若能追上,求出追上时所用的时间;若不能追上,求出甲、乙之间的最小距离
(3)请在图11中画出0~8s内甲、乙两车的速度v与时间t的图象.
分析:(1)乙车做匀加速直线运动,根据速度时间关系公式列式求解加速时间;
(2)考虑临界情况,当速度相等时,若不能追上,则间距最小;
(3)先求解出乙车的加速时间,然后做v-t图象.
(2)考虑临界情况,当速度相等时,若不能追上,则间距最小;
(3)先求解出乙车的加速时间,然后做v-t图象.
解答:解:(1)乙车做匀加速直线运动,根据速度时间关系公式,有:
t=
=
=4s
(2)乙车速度达到8m/s时,运动的位移大小为:
x2=
at2=
×2×16=16m
此时,甲运动的位移大小为:
x1=vt=8×4=32m
因为甲、乙运动的位移差为:
△x=x1-x2=16m<20m
所以,甲车不能追上乙车,且此时的距离就是最小距离其最小距离为:
xmin=20-△x=4m
(3)一次的加速时间为:t′=
=6s
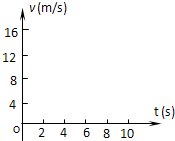
0~8s内甲、乙两车的速度v与时间t的图象如图所示:

答:(1)乙车速度增加到8m/s所用的时间为4s;
(2)甲车不能追上乙车,甲、乙之间的最小距离为4m;
(3)0~8s内甲、乙两车的速度v与时间t的图象如图所示.
t=
| v |
| a |
| 8 |
| 2 |
(2)乙车速度达到8m/s时,运动的位移大小为:
x2=
| 1 |
| 2 |
| 1 |
| 2 |
此时,甲运动的位移大小为:
x1=vt=8×4=32m
因为甲、乙运动的位移差为:
△x=x1-x2=16m<20m
所以,甲车不能追上乙车,且此时的距离就是最小距离其最小距离为:
xmin=20-△x=4m
(3)一次的加速时间为:t′=
| 12 |
| 2 |
0~8s内甲、乙两车的速度v与时间t的图象如图所示:

答:(1)乙车速度增加到8m/s所用的时间为4s;
(2)甲车不能追上乙车,甲、乙之间的最小距离为4m;
(3)0~8s内甲、乙两车的速度v与时间t的图象如图所示.
点评:本题是追赶问题,关键明确两车的运动,两部车速度相等是能否追上的临界情况.

练习册系列答案
相关题目