Question

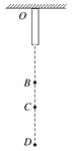
【题目】如图所示，在绝缘水平面上相距为L的A、B两点分别固定着等量正点电荷.O为AB连线的中点，C、D是AB连线上两点，其中AC=CO=OD=DB=L.一质量为m电量为+q的小滑块（可视为质点）以初动能E从C点出发，沿直线AB向D运动，滑块第一次经过O点时的动能为kE（k＞1），到达D点时动能恰好为零，小滑块最终停在O点，（已知重力加速度为g）求：

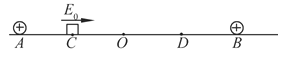
（1）小滑块与水平面之间的动摩擦因数μ.

（2）OD两点间的电势差UOD.

（3）小滑块运动的总路程x.

Answer 1

【答案】（1）（2）

【解析】解：（1）由于C点与D点等势，滑块从C到D的过程中，电场力不做功，则小滑块第一次由C到D，由动能定理有：

﹣μmg=0﹣E0

求得，小滑块与水平面间动摩擦因数为 μ=；

（2）由C第一次到O时，由动能定理得

﹣μmg+qUCO=nE0﹣E0，

解得，UCO=

（3）由C开始到最后停在O点，有：qUCO﹣μmgS=0﹣E0

由以上二式得：S=

故小滑块运动的总距离为：S=

答：

（1）小滑块与水平面之间的动摩擦因数μ为；

（2）C、O两点间的电势差UCO为．

（3）小滑块运动的总路程S为．