题目内容
一个半圆形轨道被竖直固定在水平面上，轨道两端P、Q等高，轨道半径为R，内壁光滑．现有甲、乙两个小球，球半径远小于R，甲球质量为2m，乙球质量为m，把乙球放在轨道最低点，甲球自P端由静止释放（如图）．当甲球沿轨道运动到最低点时与乙球正碰，乙球被撞后沿轨道上升到Q端．那么碰撞后甲球能沿轨道上升的高度等于（ ）分析：甲球下滑过程，机械能守恒，由机械能守恒求出甲球运动到最低点时与乙球碰撞前的速度大小，碰撞过程动量守恒，乙球碰后上滑过程，由机械能守恒求出乙球碰后的速度，根据动量守恒求得碰后甲的速度，再运用机械能守恒求得上升的高度．
解答：解：对于碰撞前甲球下滑过程，由机械能守恒定律得：
2mgR=
?2m
得v甲=
同理可得，碰后乙球获得的速度v乙=
对于碰撞过程，根据动量守恒得：
2mv甲=2mv甲′+mv乙
解得，v甲′=
对于碰后甲上滑过程，有2mgh′=
2m
得h′=
故选C
2mgR=
| 1 |
| 2 |
| v | 2 甲 |
得v甲=
| 2gR |
同理可得，碰后乙球获得的速度v乙=
| 2gR |
对于碰撞过程，根据动量守恒得：
2mv甲=2mv甲′+mv乙
解得，v甲′=
| 1 |
| 2 |
| 2gR |
对于碰后甲上滑过程，有2mgh′=
| 1 |
| 2 |
| v | ′2 甲 |
得h′=
| R |
| 4 |
故选C
点评：本题是动量守恒定律和机械能守恒定律的综合应用，分过程进行研究即可．
练习册系列答案
相关题目
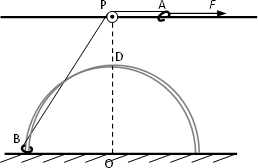
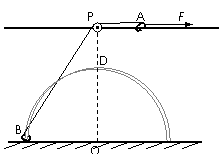
如图所示，用两根金属丝弯成一光滑半圆形轨道，竖直固定在地面上，其圆心为O、半径为0.3m．轨道正上方离地0.4m处固定一水平长直光滑杆，杆与轨道在同一竖直平面内，杆上P点处固定一定滑轮，P点位于O点正上方．A、B是质量均为2kg的小环，A套在杆上，B套在轨道上，一条不可伸长的细绳绕过定滑轮连接两环．两环均可看作质点，且不计滑轮大小与质量．现在A环上施加一个大小为55N的水平向右恒力F，使B环从地面由静止沿轨道上升．（g取10m/s2），求：
