题目内容
如图，一小滑块从固定粗糙斜面上的A点由静止下滑，经过B点下滑到底端C点时速度恰好为零．已知斜面倾角为37°，滑块与AB段的动摩擦因数为0.5，与BC段的动摩擦因数为0.8，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8，则AB段和BC段的长度之比为（ ）分析：先受力分析，根据牛顿第二定律求出两段的加速度，再根据速度位移公式列式分析求解．
解答：解：对物体，加速下滑时，有
mgsinθ-μ1mgcosθ=ma1
解得
a1=g（sinθ-μ1gcosθ）=2m/s2
物体减速下滑时，有
mgsinθ-μ2mgcosθ=ma2
解得
a2=g（sinθ-μ2gcosθ）=-0.4m/s2
假设最大速度为v，加速过程的位移为
x1=
减速过程的位移为
x2=
故
=
=
故选A．
mgsinθ-μ1mgcosθ=ma1
解得
a1=g（sinθ-μ1gcosθ）=2m/s2
物体减速下滑时，有
mgsinθ-μ2mgcosθ=ma2
解得
a2=g（sinθ-μ2gcosθ）=-0.4m/s2
假设最大速度为v，加速过程的位移为
x1=
| v2 |
| 2a1 |
减速过程的位移为
x2=
| v2 |
| 2a2 |
故
| x1 |
| x2 |
| a2 |
| a1 |
| 1 |
| 5 |
故选A．
点评：本题关键是对物体受力分析，根据牛顿第二定律求出加速度，然后根据速度位移公式列式求解位移之比．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
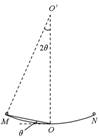
如图，一小滑块从固定粗糙斜面上的A点由静止下滑，经过B点下滑到底端C点时速度恰好为零．已知斜面倾角为37°，滑块与AB段的动摩擦因数为0.5，与BC段的动摩擦因数为0.8，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8，则AB段和BC段的长度之比为