题目内容
14. 总长为L的气缸用质量为m的活塞封有一定质量的理想气体,当气缸水平横放时,空气柱长为l0,如图1所示,现将气缸按图2竖直放置,已知大气压强为P0,活塞横截面积为S,它与气缸之间无摩擦且不漏气,气体温度T0保持不变,求:
总长为L的气缸用质量为m的活塞封有一定质量的理想气体,当气缸水平横放时,空气柱长为l0,如图1所示,现将气缸按图2竖直放置,已知大气压强为P0,活塞横截面积为S,它与气缸之间无摩擦且不漏气,气体温度T0保持不变,求:(ⅰ)气缸竖直放置时空气柱长度;
(ⅱ)气缸开口向上竖直放置时,若将密闭气体缓慢加热,活塞刚好到达气缸开口端,求密闭气体温度T.
分析 (1)以活塞为研究对象,求出气缸中封闭气体的压强,根据玻意耳定律列式求解
(2)升温膨胀过程中,气体发生等压变化,根据盖-吕萨克定律列式求解
解答 解:(1)汽缸水平放置时${p}_{1}^{\;}={p}_{0}^{\;}$,${V}_{1}^{\;}={l}_{0}^{\;}S$
汽缸竖直放置时,${p}_{0}^{\;}S+mg={p}_{2}^{\;}S$,得${p}_{2}^{\;}={p}_{0}^{\;}+\frac{mg}{S}$,${V}_{2}^{\;}={l}_{1}^{\;}S$
据玻意耳定律得${p}_{1}^{\;}{V}_{1}^{\;}={p}_{2}^{\;}{V}_{2}^{\;}$
${p}_{0}^{\;}{l}_{0}^{\;}S=({p}_{0}^{\;}+\frac{mg}{S}){l}_{1}^{\;}S$
解得:${l}_{1}^{\;}=\frac{{p}_{0}^{\;}{l}_{0}^{\;}S}{{p}_{0}^{\;}S+mg}$
(2)缓慢加热,发生等压变化
$\frac{{l}_{0}^{\;}S}{{T}_{0}^{\;}}=\frac{LS}{T}$
解得:$T=\frac{L}{{l}_{0}^{\;}}{T}_{0}^{\;}$
答:(ⅰ)气缸竖直放置时空气柱长度为$\frac{{p}_{0}^{\;}{l}_{0}^{\;}S}{{p}_{0}^{\;}S+mg}$;
(ⅱ)气缸开口向上竖直放置时,若将密闭气体缓慢加热,活塞刚好到达气缸开口端,求密闭气体温度T为$\frac{L}{{l}_{0}^{\;}}{T}_{0}^{\;}$
点评 本题考查理想气体的实验定律,在解题时要注意明确三个状态参量中哪个量是不变的,从而选择正确的规律求解.

 综合自测系列答案
综合自测系列答案| A. | 1J=1kW•h | B. | 1J=1kg•m/s2•m | C. | 1J=1W•s | D. | 1J=1N•m |
| A. | 库仑认为电荷的周围存在着由它产生的电场 | |
| B. | 自然界的电荷只有两种,美国科学家富兰克林把它们命名为正电荷和负电荷 | |
| C. | 电场力的方向就是电场强度的方向 | |
| D. | 电场强度的大小和电荷所受的电场力的大小成正比 |
| A. | 公式E=$\frac{kQ}{r^2}$适用于任何带电体周围的电场 | |
| B. | 电场中某一点的场强与该点放不放试探电荷无关 | |
| C. | 由公式E=$\frac{F}{q}$可知,电场中某点的场强大小E与q成反比,与F成正比 | |
| D. | 正、负试探电荷在电场中同一点受到的电场力方向相反,所以场强方向与放入试探电荷的正负有关 |
 在《共点的两个力的合成》的实验中,得到了如图所示的图形,图中P为橡皮条的固定点,O为橡皮条与细线的结点,用两只弹簧秤或用一只弹簧秤时,都将结点拉到O点,实验中你要比较的是图中F3 和F4 两个力的大小和方向,其中F4是实验直接测得的合力.
在《共点的两个力的合成》的实验中,得到了如图所示的图形,图中P为橡皮条的固定点,O为橡皮条与细线的结点,用两只弹簧秤或用一只弹簧秤时,都将结点拉到O点,实验中你要比较的是图中F3 和F4 两个力的大小和方向,其中F4是实验直接测得的合力.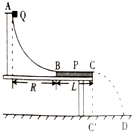 如图所示,AB是半径为R的四分之一光滑圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,BC的长度为L,C点在水平地面的垂直投影为C′,CC′的高度为h.一小物块(可视为质点)Q从轨道上的A点由静止释放,最后落在D点,C′D的距离为s.重力加速度为g,不计空气阻力.求:
如图所示,AB是半径为R的四分之一光滑圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,BC的长度为L,C点在水平地面的垂直投影为C′,CC′的高度为h.一小物块(可视为质点)Q从轨道上的A点由静止释放,最后落在D点,C′D的距离为s.重力加速度为g,不计空气阻力.求: 滑雪运动是2022年北京冬季奥运会运动项目之一,受到众多年轻人的喜爱.如图所示,质量为60kg的滑雪运动员,在倾角为30°的斜坡顶端,从静止开始匀加速下滑90m到达坡底,用时10s.若g取10m/s2,求运动员:
滑雪运动是2022年北京冬季奥运会运动项目之一,受到众多年轻人的喜爱.如图所示,质量为60kg的滑雪运动员,在倾角为30°的斜坡顶端,从静止开始匀加速下滑90m到达坡底,用时10s.若g取10m/s2,求运动员: