题目内容
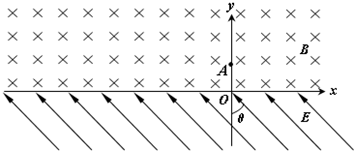
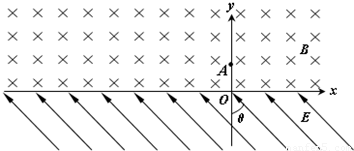
在如图所示,x轴上方有一匀强磁场,磁感应强度的方向垂直于纸面向里,大小为B,x轴下方有一匀强电场,电场强度的大小为E,方向与y轴的夹角θ为45°且斜向上方.现有一质量为m、电量为q的正离子,以速度v由y轴上的A点沿y轴正方向射入磁场,该离子在磁场中运动一段时间后从x轴上的C点进入电场区域,该离子经C点时的速度方向与x轴夹角为45°.不计离子的重力,设磁场区域和电场区域足够大. 求:(1)C点的坐标;
(2)离子从A点出发到第三次穿越x轴时的运动时间;
(3)离子第四次穿越x轴时速度的大小及速度方向与电场方向的夹角.
【答案】分析:(1)带电粒子在匀强磁场中在洛仑兹力作用下做匀速圆周运动,由牛顿第二定律求出轨迹半径.画出粒子运动的轨迹,由几何知识求出C点的坐标;
(2)粒子从A运动C,转过225°角.第一次进入电场后,粒子先做匀减速直线运动,速度减到零后做匀加速直线运动返回,第二次穿越x轴,进入磁场后,转过90°第二次穿越x轴进入电场.根据时间与周期的关系求出在磁场运动的时间.由牛顿定律和运动学公式求解在电场中运动的时间,再求出总时间.
(3)粒子从第三次过x轴到第四次过x轴的过程是在电场中做类平抛的运动,采用运动的分解,由牛顿定律和运动学公式求解第四次穿越x轴时速度的大小及速度方向与电场方向的夹角.
解答:解:(1)磁场中带电粒子在洛仑兹力作用下做匀速圆周运动,故有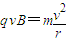 得
得 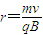
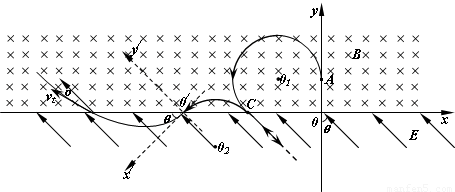
粒子运动轨迹如图所示,由几何知识知,
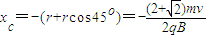
故C点坐标为(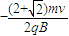 ,0)
,0)
(2)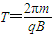
设粒子从A到C的时间为t1,由几何知识知: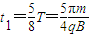
设粒子从进入电场到返回C的时间为t2,其在电场中做匀变速运动,由牛顿第二定律和运动学公式,有
qE=ma 及2v=at2
联立(6)(7)解得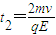
设粒子再次进入磁场后在磁场中运动的时间为t3,由题意知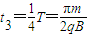
所以粒子从A点到第三次穿越x轴的时间为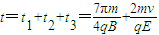
(3)粒子从第三次过x轴到第四次过x轴的过程是在电场中做类平抛的运动,即沿着v的方向(设为x′轴)以v做匀速运动,沿着qE的方向(设为y′轴)做初速度为0的匀加速运动
即x'=vt
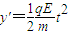
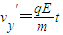
设离子第四次穿越x轴时速度的大小为v,速度方向与电场方向的夹角为α.
由图中几何关系知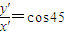
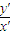 =cos45°,v=
=cos45°,v=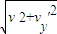 ,
,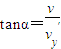
综合上述得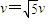 ,
,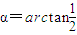
答:(1)C点的坐标是(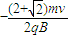 ,0);
,0);
(2)离子从A点出发到第三次穿越x轴时的运动时间是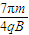 +
+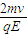 ;
;
(3)离子第四次穿越x轴时速度的大小为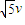 ,速度方向与电场方向的夹角
,速度方向与电场方向的夹角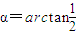 .
.
点评:本题是粒子在电场和磁场中运动的问题,电场中类平抛运动的研究方法是运动的分解,磁场中圆周运动的研究方法是画轨迹.
(2)粒子从A运动C,转过225°角.第一次进入电场后,粒子先做匀减速直线运动,速度减到零后做匀加速直线运动返回,第二次穿越x轴,进入磁场后,转过90°第二次穿越x轴进入电场.根据时间与周期的关系求出在磁场运动的时间.由牛顿定律和运动学公式求解在电场中运动的时间,再求出总时间.
(3)粒子从第三次过x轴到第四次过x轴的过程是在电场中做类平抛的运动,采用运动的分解,由牛顿定律和运动学公式求解第四次穿越x轴时速度的大小及速度方向与电场方向的夹角.
解答:解:(1)磁场中带电粒子在洛仑兹力作用下做匀速圆周运动,故有
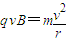 得
得 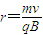

粒子运动轨迹如图所示,由几何知识知,
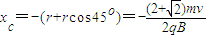
故C点坐标为(
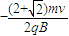 ,0)
,0)(2)
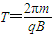
设粒子从A到C的时间为t1,由几何知识知:
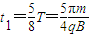
设粒子从进入电场到返回C的时间为t2,其在电场中做匀变速运动,由牛顿第二定律和运动学公式,有
qE=ma 及2v=at2
联立(6)(7)解得
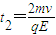
设粒子再次进入磁场后在磁场中运动的时间为t3,由题意知
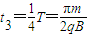
所以粒子从A点到第三次穿越x轴的时间为
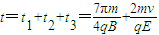
(3)粒子从第三次过x轴到第四次过x轴的过程是在电场中做类平抛的运动,即沿着v的方向(设为x′轴)以v做匀速运动,沿着qE的方向(设为y′轴)做初速度为0的匀加速运动
即x'=vt
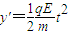
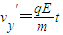
设离子第四次穿越x轴时速度的大小为v,速度方向与电场方向的夹角为α.
由图中几何关系知
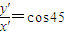
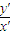 =cos45°,v=
=cos45°,v=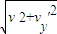 ,
,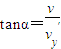
综合上述得
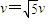 ,
,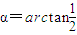
答:(1)C点的坐标是(
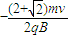 ,0);
,0);(2)离子从A点出发到第三次穿越x轴时的运动时间是
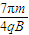 +
+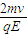 ;
;(3)离子第四次穿越x轴时速度的大小为
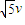 ,速度方向与电场方向的夹角
,速度方向与电场方向的夹角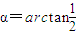 .
.点评:本题是粒子在电场和磁场中运动的问题,电场中类平抛运动的研究方法是运动的分解,磁场中圆周运动的研究方法是画轨迹.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目