题目内容
如图所示，正方形导线框abcd的质量为m、边长为l，导线框的总电阻为R．导线框从垂直纸面向里的水平有界匀强磁场的上方某处由静止自由下落，下落过程中，导线框始终在与磁场垂直的竖直平面内，cd边保持水平．磁场的磁感应强度大小为B，方向垂直纸面向里，磁场上、下两个界面水平距离为2l．已知cd边刚进入磁场时线框恰好做匀速运动．重力加速度为g．求：（1）释放线框时cd边距磁场上边界的高度．
（2）cd边刚要离开磁场下边界时线框的动能．
（3）线框cd边刚刚离开磁场下边界时线框的加速度．
分析：（1）cd边刚进入磁场时做匀速直线运动，则重力等于安培力，根据平衡求出线框的速度，通过速度位移公式求出释放线框时cd边距磁场上边界的高度．
（2）根据动能定理求出cd边刚要离开磁场下边界时的动能．
（3）求出此时的速度，从而结合切割产生的感应电动势公式、安培力公式、闭合电路欧姆定律，求出安培力的大小，根据牛顿第二定律求出线框的加速度．
（2）根据动能定理求出cd边刚要离开磁场下边界时的动能．
（3）求出此时的速度，从而结合切割产生的感应电动势公式、安培力公式、闭合电路欧姆定律，求出安培力的大小，根据牛顿第二定律求出线框的加速度．
解答：解：（1）根据mg=BIL，I=
解得mg=
则v=
根据速度位移公式得，h=
=
．
（2）根据动能定理得，mgl=Ek-
mv2
解得Ek=mgl+
．
（3）因为
mv′2=mgl+
．
解得cd边到达磁场下边界的速度v′=
．
则安培力F=BIl=
根据牛顿第二定律得，a=
=
-g．
答：（1）释放线框时cd边距磁场上边界的高度
．
（2）cd边刚要离开磁场下边界时线框的动能Ek=mgl+
．
（3）线框cd边刚刚离开磁场下边界时线框的加速度
-g．
| BLv |
| R |
解得mg=
| B2l2v |
| R |
则v=
| mgR |
| B2l2 |
根据速度位移公式得，h=
| v2 |
| 2g |
| m2R2g |
| 2B4l4 |
（2）根据动能定理得，mgl=Ek-
| 1 |
| 2 |
解得Ek=mgl+
| m3R2g2 |
| 2B4l4 |
（3）因为
| 1 |
| 2 |
| m3R2g2 |
| 2B4l4 |
解得cd边到达磁场下边界的速度v′=
2gl+
|
则安培力F=BIl=
B2l2
| ||||
| R |
根据牛顿第二定律得，a=
| F-mg |
| m |
B2l2
| ||||
| mR |
答：（1）释放线框时cd边距磁场上边界的高度
| m2R2g |
| 2B4l4 |
（2）cd边刚要离开磁场下边界时线框的动能Ek=mgl+
| m3R2g2 |
| 2B4l4 |
（3）线框cd边刚刚离开磁场下边界时线框的加速度
B2l2
| ||||
| mR |
点评：本题考查电磁感应与力学和功能的综合，知道线框匀速运动时，安培力与重力平衡，结合切割产生的感应电动势公式、安培力公式、闭合电路欧姆定律进行求解．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
如图所示，正方形导线框abcd的质量为m、边长为l，导线框的总电阻为R．导线框从垂直纸面向里的水平有界匀强磁场的上方某处由静止自由下落，下落过程中，导线框始终在与磁场垂直的竖直平面内，cd边保持水平．磁场的磁感应强度大小为B，方向垂直纸面向里，磁场上、下两个界面水平距离为l．已知cd边刚进入磁场时线框恰好做匀速运动．重力加速度为g．
如图所示，正方形导线框ABCD之边长l=10cm，质量m=50g，电阻R=0.1Ω．让线框立在地面上，钩码质量m′=70g，用不可伸长的细线绕过两个定滑轮，连接线框AB边的中点和钩码，线框上方某一高度以上有匀强磁场B=1.0T．当钩码由图示位置被静止释放后，线框即被拉起，上升到AB边进入磁场时就作匀速运动．细绳质量、绳与滑轮间的摩擦和空气阻力均不计，g取10m/s2，求：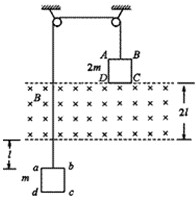
如图所示，正方形导线框ABCD、abcd的边长均为L，电阻均为R，质量分别为2m、m，它们分别系在一跨过两个定滑轮的轻绳两端，且正方形导线框与定滑轮处于同一竖直平面内．在两导线框之间有一宽度为2L、磁感应强度大小为B、方向垂直纸面向里的匀强磁场，开始时导线框ABCD的下边与匀强磁场的上边界重合，导线框abcd的上边到匀强磁场的下边界的距离为L．现将系统由静止释放，当导线框ABCD刚好全部进入磁场时，系统开始做匀速运动，不计摩擦的空气阻力，则（ ）
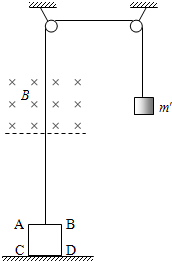如图所示，正方形导线框ABCD之边长l=10cm，质量m=50g，电阻R=0.1Ω．让线框立在地面上，钩码质量m′=70g，用不可伸长的细线绕过两个定滑轮，连接线框AB边的中点和钩码，线框上方某一高度以上有匀强磁场B=1.0T．当钩码由图示位置被静止释放后，线框即被拉起，上升到AB边进入磁场时就作匀速运动．细绳质量、绳与滑轮间的摩擦和空气阻力均不计，g取10m/s2，求：
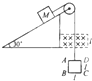如图所示，正方形导线框ABCD每边长为0.2m，线框电阻R=0.1欧姆，质量m=0.1kg，物体M的质量为0.3kg，匀强有界磁场高也为0.2m，B=0.5Tm．物体M放在光滑斜面上，斜面倾角为30°．物体从静止开始下滑，当线框AD边进入磁场时，恰好开始做匀速运动．求：（g取10m/s2）