题目内容
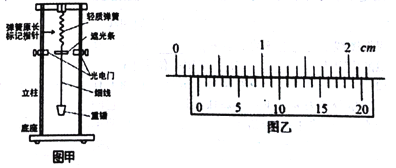
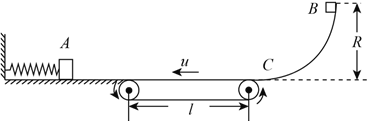
【题目】如图所示为某种弹射装置的示意图，该装置由三部分组成，传送带左边是足够长的光滑水平面，一轻质弹簧左端固定，右端连接着质量
的物块
．装置的中间是水平传送带，它与左右两边的台面等高，并能平滑对接．传送带的皮带轮逆时针匀速转动，使传送带上表面以
匀速运动．传送带的右边是一半径
位于竖直平面内的光滑
圆弧轨道．质量
的物块
从
圆弧的最高处由静止释放．已知物导体
与传送带之间动摩擦因数
，传送带两轴之间的距离
．设物块
、
之间发生的是正对弹性碰撞，第一次碰撞前，物块
静止．取
．求：
（1）物块
滑动
圆弧的最低点
时对轨道的压力．
（2）物块
与物块
第一次碰撞前的速度大小．
（3）物块
与物块
第一次碰撞后瞬间的各自的速度大小．
（4）物块
与物块
第一碰撞后弹簧的最大弹性势能．
（5）计算说明物块
是否能够回到
段圆弧上．
（6）物块
第一次碰撞后第二次碰撞前，在传送带上运动的时间．
（7）如果物块
、
每次碰撞后，物块
再回到平衡位置时弹簧都会被立即锁定，而当它们再次碰撞前锁定解除，求物块
经第一次与物块
碰撞后在传送带上运动的总时间．
【答案】（1）
（2）
（3）
（4）
（5）回不到（6）
（7）
【解析】解：(1)依据动能定理
根据牛二定律
再根据牛三定律
，故压力大小为
．
(2)由题可得
，依据受力分析可知
解得
若物块一直做匀减速直线运动，依据运动学公式
当
时，解得
，即
，故碰撞前的速度
．
(3)依据动量定理
依据能量守恒
，
解得： 
， 
，所以各自的速度大小都为
．
(4)依据能量守恒
（
）．
(5) 
物块返回后，做减速运动且
加速度
，
做匀减速运动，当速度为
时， 
可知
，故回不到
的圆弧上
(6)依据运动学公式
故运动过去时
回来时
，
总时间
．
(7)依据几何关系第一次
，
第二次
第三次
，
时间
为等比数列， 
，故
，
当
时， 
练习册系列答案
相关题目
