题目内容
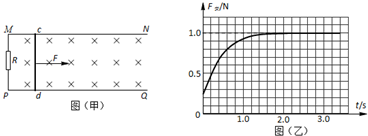 (2012?虹口区二模)如图(甲)所示,MN、PQ为水平放置的足够长的平行光滑导轨,导轨间距L为0.5m,导轨左端连接一个阻值为2Ω的定值电阻R,将一根质量为0.2kg的金属棒cd垂直放置在导轨上,且与导轨接触良好,金属棒cd的电阻r=2Ω,导轨电阻不计,整个装置处于垂直导轨平面向下的匀强磁场中,磁感应强度为B=2T.若棒以1m/s的初速度向右运动,同时对棒施加水平向右的拉力F作用,并保持拉力的功率恒为4W,从此时开始计时,经过一定时间t金属棒的速度稳定不变,电阻R中产生的电热为3.2J,图(乙)为安培力与时间的关系图象.试求:
(2012?虹口区二模)如图(甲)所示,MN、PQ为水平放置的足够长的平行光滑导轨,导轨间距L为0.5m,导轨左端连接一个阻值为2Ω的定值电阻R,将一根质量为0.2kg的金属棒cd垂直放置在导轨上,且与导轨接触良好,金属棒cd的电阻r=2Ω,导轨电阻不计,整个装置处于垂直导轨平面向下的匀强磁场中,磁感应强度为B=2T.若棒以1m/s的初速度向右运动,同时对棒施加水平向右的拉力F作用,并保持拉力的功率恒为4W,从此时开始计时,经过一定时间t金属棒的速度稳定不变,电阻R中产生的电热为3.2J,图(乙)为安培力与时间的关系图象.试求:(1)金属棒的最大速度;
(2)金属棒速度为2m/s时的加速度;
(3)此过程对应的时间t;
(4)估算0~3s内通过电阻R的电量.
分析:(1)当金属棒所受的拉力和安培力相等时,受到最大,根据P=Fvm,F=BIL联立求出金属棒的最大速度.
(2)求出金属棒速度为2m/s时的感应电动势,从而求出感应电流的大小,根据F=BIL求出安培力的大小,再通过牛顿第二定律求出加速度的大小.
(3)克服安培力做的功全部转化为整个回路的热量,通过电阻R中产生的电热求出整个回路产生的电热,根据动能定理,通过拉力做功W=Pt求出此过程对应的时间.
(4)因为△q=I△t=
△t,根据图线所围成的面积求出FA△t,从而得出0~3s内通过电阻R的电量.
(2)求出金属棒速度为2m/s时的感应电动势,从而求出感应电流的大小,根据F=BIL求出安培力的大小,再通过牛顿第二定律求出加速度的大小.
(3)克服安培力做的功全部转化为整个回路的热量,通过电阻R中产生的电热求出整个回路产生的电热,根据动能定理,通过拉力做功W=Pt求出此过程对应的时间.
(4)因为△q=I△t=
| FA |
| BL |
解答:解:(1)金属棒的速度最大时,所受的合外力为零,即F=BIL.
而P=Fvm,I=
解出:vm=
=
m/s=4m/s.
(2)速度为2m/s时,感应电动势E=BLv=2×0.5×2V=2V,
电流I=
=
A=0.5A,
安培力F安=BIL=2×0.5×0.5N=0.5N.
金属棒受到的拉力F=
=
N=2N
根据牛顿第二定律:F-F安=ma
解得a=
=
m/s2=7.5m/s2.
(3)在此过程中,由动能定理得:
Pt+W安=
mvm2-
mv02
而W安=-(QR+Qr)=-2QR=-6.4J.
解出t=
=
s=1.975s.
(4)图线与横轴之间共有124+15×
=131.5个小方格.
相应的面积为131.5×0.2×0.1N.s=2.63N.s,即
F安△t=2.63N.s
故q=
I.△t=
=
C=2.63C.
答:(1)金属棒的最大速度为4m/s.
(2)金属棒速度为2m/s时的加速度为7.5m/s2.
(3)此过程对应的时间t为1.975s.
(4)0~3s内通过电阻R的电量2.63C.
而P=Fvm,I=
| BLvm |
| R+r |
解出:vm=
| ||
| BL |
| ||
| 2×0.5 |
(2)速度为2m/s时,感应电动势E=BLv=2×0.5×2V=2V,
电流I=
| E |
| R+r |
| 2 |
| 2+2 |
安培力F安=BIL=2×0.5×0.5N=0.5N.
金属棒受到的拉力F=
| P |
| v |
| 4 |
| 2 |
根据牛顿第二定律:F-F安=ma
解得a=
| F-F安 |
| m |
| 2-0.5 |
| 0.2 |
(3)在此过程中,由动能定理得:
Pt+W安=
| 1 |
| 2 |
| 1 |
| 2 |
而W安=-(QR+Qr)=-2QR=-6.4J.
解出t=
| mvm2-mv02-2W安 |
| 2P |
| 0.2×42-0.2×12+2×6.4 |
| 2×4 |
(4)图线与横轴之间共有124+15×
| 1 |
| 2 |
相应的面积为131.5×0.2×0.1N.s=2.63N.s,即
 |
故q=
 |
| |||
| BL |
| 2.63 |
| 2×0.5 |
答:(1)金属棒的最大速度为4m/s.
(2)金属棒速度为2m/s时的加速度为7.5m/s2.
(3)此过程对应的时间t为1.975s.
(4)0~3s内通过电阻R的电量2.63C.
点评:本题综合考查了牛顿第二定律、动能定理、功能关系等知识,综合性较强,对学生能力的要求较高,是一道好题.

练习册系列答案
相关题目
 (2012?虹口区二模)如图所示,在柱形容器中装有部分水,容器上方有一可自由移动的活塞.容器水面浮有一个木块和一个一端封闭、开口向下的玻璃管,玻璃管中有部分空气,系统稳定时,玻璃管内空气柱在管外水面上方的长度为a,空气柱在管外水面下方的长度为b,水面上方木块的高度为c,水面下方木块的高度为d.现在活塞上方施加竖直向下、且缓缓增大的力F,使活塞下降一小段距离(未碰及玻璃管和木块),下列说法中正确的是( )
(2012?虹口区二模)如图所示,在柱形容器中装有部分水,容器上方有一可自由移动的活塞.容器水面浮有一个木块和一个一端封闭、开口向下的玻璃管,玻璃管中有部分空气,系统稳定时,玻璃管内空气柱在管外水面上方的长度为a,空气柱在管外水面下方的长度为b,水面上方木块的高度为c,水面下方木块的高度为d.现在活塞上方施加竖直向下、且缓缓增大的力F,使活塞下降一小段距离(未碰及玻璃管和木块),下列说法中正确的是( ) (2012?虹口区二模)在水平放置的光滑绝缘杆ab上,挂有两个金属环M和N,两环套在一个通电密绕长螺线管的中部,螺线管中部区域的管外磁场可以忽略.当变阻器的滑动头向左移动时,两环的运动情况是( )
(2012?虹口区二模)在水平放置的光滑绝缘杆ab上,挂有两个金属环M和N,两环套在一个通电密绕长螺线管的中部,螺线管中部区域的管外磁场可以忽略.当变阻器的滑动头向左移动时,两环的运动情况是( )