题目内容
质量为M、长为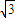 L的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳,绳上套着一质量为m的小铁环.已知重力加速度为g,不计空气影响.
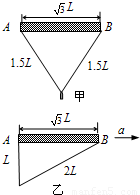
L的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳,绳上套着一质量为m的小铁环.已知重力加速度为g,不计空气影响.(1)现让杆和环均静止悬挂在空中,如图甲,求绳中拉力的大小:
(2)若杆与环保持相对静止,在空中沿AB方向水平向右做匀加速直线运动,此时环恰好悬于A端的正下方,如图乙所示.
①求此状态下杆的加速度大小a;
②为保持这种状态需在杆上施加一个多大的外力,方向如何?
【答案】分析:(1)以环为研究对象,环处于静止状态,合力为零,根据平衡条件求解绳中拉力的大小;
(2)①以环为研究对象,由正交分解法,根据牛顿第二定律求解加速度;
②对整体研究,由正交分解法,根据牛顿第二定律求解外力的大小和方向.
解答: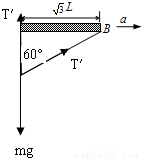 解:(1)以环为研究对象,环处于静止状态,合力为零,设两绳的夹角为2θ.
解:(1)以环为研究对象,环处于静止状态,合力为零,设两绳的夹角为2θ.
则sinθ=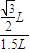 =
=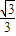 ,得cosθ=
,得cosθ=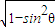 =
=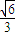
设绳子的拉力大小为T,由平衡条件得
2Tcosθ=mg
解得,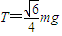
(2)①对环:设绳子的拉力大小为T′,则根据牛顿第二定律得:
竖直方向:T′+T′cos60°=mg
水平方向:T′sin60°=ma,
解得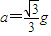
②设外力大小为F,方向与水平方向成α角斜向右上方.
对整体:由牛顿第二定律得:
水平方向:Fcosα=(M+m)a
竖直方向:Fsinα=(M+m)g
解得,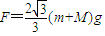 ,α=60°即外力方向与水平方向夹角为60°斜向右上方.
,α=60°即外力方向与水平方向夹角为60°斜向右上方.
答:(1)现让杆和环均静止悬挂在空中,绳中拉力的大小是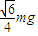 ;
;
(2)①此状态下杆的加速度大小a为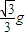 ;
;
②为保持这种状态需在杆上施加一个的外力为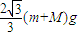 ,方向与水平方向夹角为60°斜向右上方.
,方向与水平方向夹角为60°斜向右上方.
点评:本题中铁环与动滑轮相似,两侧绳子拉力大小相等,运用正交分解法研究平衡状态和非平衡情况.
(2)①以环为研究对象,由正交分解法,根据牛顿第二定律求解加速度;
②对整体研究,由正交分解法,根据牛顿第二定律求解外力的大小和方向.
解答:
 解:(1)以环为研究对象,环处于静止状态,合力为零,设两绳的夹角为2θ.
解:(1)以环为研究对象,环处于静止状态,合力为零,设两绳的夹角为2θ.则sinθ=
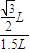 =
=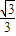 ,得cosθ=
,得cosθ=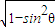 =
=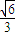
设绳子的拉力大小为T,由平衡条件得
2Tcosθ=mg
解得,
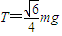
(2)①对环:设绳子的拉力大小为T′,则根据牛顿第二定律得:
竖直方向:T′+T′cos60°=mg
水平方向:T′sin60°=ma,
解得
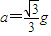
②设外力大小为F,方向与水平方向成α角斜向右上方.
对整体:由牛顿第二定律得:
水平方向:Fcosα=(M+m)a
竖直方向:Fsinα=(M+m)g
解得,
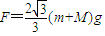 ,α=60°即外力方向与水平方向夹角为60°斜向右上方.
,α=60°即外力方向与水平方向夹角为60°斜向右上方.答:(1)现让杆和环均静止悬挂在空中,绳中拉力的大小是
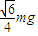 ;
;(2)①此状态下杆的加速度大小a为
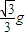 ;
;②为保持这种状态需在杆上施加一个的外力为
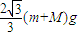 ,方向与水平方向夹角为60°斜向右上方.
,方向与水平方向夹角为60°斜向右上方.点评:本题中铁环与动滑轮相似,两侧绳子拉力大小相等,运用正交分解法研究平衡状态和非平衡情况.

练习册系列答案
相关题目
 如图所示,质量为m、长为L的均匀细杆OA,一端通过光滑铰链固定在地面O处,在细杆中点B处系一根细绳,细绳绕过两个光滑定滑轮后悬挂着物体D,物体D的质量为细杆质量的1/3,D离滑轮距离足够远.在外力F的作用下使细杆与地面保持夹角θ为60°,此时细绳CB与杆的夹角也为60°(如图所示).已知细杆绕O点转动的动能表达式为
如图所示,质量为m、长为L的均匀细杆OA,一端通过光滑铰链固定在地面O处,在细杆中点B处系一根细绳,细绳绕过两个光滑定滑轮后悬挂着物体D,物体D的质量为细杆质量的1/3,D离滑轮距离足够远.在外力F的作用下使细杆与地面保持夹角θ为60°,此时细绳CB与杆的夹角也为60°(如图所示).已知细杆绕O点转动的动能表达式为





 =
= 
















