题目内容
如图所示，在竖直向下的磁感应强度为B的匀强磁场中，有两根水平放置且足够长的平行金属导轨AB、CD，间距为L，在导轨的AC端连接一阻值为R的电阻，一根质量为m的金属棒ab，垂直导轨放置，导轨和金属棒的电阻不计．金属棒与导轨间的动摩擦因数为μ，若用恒力F沿水平向右拉导体棒运动，求金属棒的最大速度．分析：金属棒ab从静止开始沿导轨滑动，从而产生感应电流，出现安培力，金属棒先做加速度逐渐减小的加速运动，后做匀速运动．根据E=BLv、I=
和F=BIL推导出安培力公式，当加速度减小到0时，达到最大速度，由平衡条件求出最大速度．
| E |
| R |
解答：解：经分析知，棒向右运动时切割磁感线，产生动生电动势，由右手定则知，棒中有ab方向的电流，再由左手定则可知，安培力向左，棒受到的合力在减小，向右做加速度逐渐减小的加速运动，当安培力与摩擦力的合力增大到大小等于拉力时，则加速度减小到0时，达到最大速度，此时：
F=μmg+BIL
又I=
解得 vm=
；
答：金属棒的最大速度
．
F=μmg+BIL
又I=
| BLv |
| R |
解得 vm=
| (F-μmg)R |
| B2L2 |
答：金属棒的最大速度
| (F-μmg)R |
| B2L2 |
点评：本题要根据牛顿定律分析金属棒的运动情况，分析和计算安培力是关键，注意另忘记棒受到摩擦力作用．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图所示，在竖直向下场强大小为E的匀强电场中，有一光滑绝缘半圆环在其上端一个质量为m、带电量为+q的小球由静止开始沿轨道运动，则（ ）
如图所示，在竖直向下的匀强电场中有一绝缘的光滑离心轨道，一个带负电的小球从斜轨道上的A点由静止释放，沿轨道滑下，已知小球的质量为m=1kg，电量大小为q=6×10-4C，匀强电场的场强大小为E=1×104N/C，斜轨道的倾角为α=30°，圆轨道半径R=0.8m，（小球的重力大于所受的电场力g=10m/s2）．
如图所示，在竖直向下的匀强磁场中，将一个水平放置的金属棒ab以水平初速度V0抛出，设运动的整个过程中棒的取向不变且不计空气阻力，则金属棒在运动过程中产生的感应电动势大小将（ ）
（2009?奉贤区二模）如图所示，在竖直向下的匀强磁场中，有两根竖直放置的平行导轨AB、CD，导轨上放有质量为m的金属棒MN，棒与导轨间的动摩擦因数为u，现从t=0时刻起，给棒通以图示方向的电流，且电流强度与时间成正比，即I=kt，其中k为恒量．若金属棒与导轨始终垂直，则下图所示的表示棒所受的摩擦力随时间变化的四幅图中，正确的是（ ）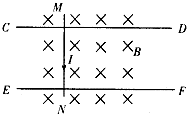
如图所示，在竖直向下的匀强磁场中有两根水平放置的平行粗糙导轨CD、EF，导轨上放有一金属棒MN．现从t=0时刻起，给棒通以图示方向的电流且电流强度与时间成正比，即I=kt，其中k为常量，金属棒与导轨始终垂直且接触良好．下列关于棒的速度v、加速度a随时间t变化的关系图象，可能正确的是（ ）