题目内容
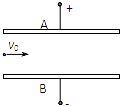 如图,质量m=5×10-8kg的带负电微粒以v0=2m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长L=10cm,板间距离d=2cm.当U0=1000V时,带电粒子恰好沿线穿过板间,取g=10m/s2,求:
如图,质量m=5×10-8kg的带负电微粒以v0=2m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长L=10cm,板间距离d=2cm.当U0=1000V时,带电粒子恰好沿线穿过板间,取g=10m/s2,求:(1)带电粒子的电量.
(2)当电压为U1=800V时,粒子离开金属板时的竖直偏转位移.
(3)当电压为U2=2000V时,该电场最终对粒子所做的功.
分析:(1)粒子受重力和电场力,做匀速直线运动,处于平衡状态,根据平衡条件求解粒子的电量;
(2)当电压为U1=800V时,先根据牛顿第二定律求解加速度,然后根据类似平抛运动的分位移公式列式求解;
(3)先类似平抛运动的分位移公式求解粒子恰好从上边缘飞出的临界电压;然后再根据类似平抛运动的分位移公式列式求解.
(2)当电压为U1=800V时,先根据牛顿第二定律求解加速度,然后根据类似平抛运动的分位移公式列式求解;
(3)先类似平抛运动的分位移公式求解粒子恰好从上边缘飞出的临界电压;然后再根据类似平抛运动的分位移公式列式求解.
解答:解:(1)由电场力和重力平衡得到:
mg=qE
其中:
E=
解得:
q=
=
=10-11C
(2)当电压为U1=800V时,根据类似平抛运动的分位移公式,有:
y=
at2
L=v0t
根据牛顿第二定律,有:
a=g-
联列解得:y=2.3×10-3m
(3)当电压较大时,粒子向上偏,既可以从两极板穿出,也可能打在上极板上;
假设粒子刚好从上极板射出,根据类似平抛运动的分位移公式,有:
=
(
-g)(
)2
解得:U=1800V,所以,当电压为U2=2000V时,粒子打在上极板
此时:W=q(
)=10-8J
答:(1)带电粒子的电量为10-11C.
(2)当电压为U1=800V时,粒子离开金属板时的竖直偏转位移为2.3×10-3m.
(3)当电压为U2=2000V时,该电场最终对粒子所做的功为10-8J.
mg=qE
其中:
E=
| U |
| d |
解得:
q=
| mgd |
| U |
| 5×10-8×10×0.02 |
| 1000 |
(2)当电压为U1=800V时,根据类似平抛运动的分位移公式,有:
y=
| 1 |
| 2 |
L=v0t
根据牛顿第二定律,有:
a=g-
| qU |
| md |
联列解得:y=2.3×10-3m
(3)当电压较大时,粒子向上偏,既可以从两极板穿出,也可能打在上极板上;
假设粒子刚好从上极板射出,根据类似平抛运动的分位移公式,有:
| d |
| 2 |
| 1 |
| 2 |
| qU |
| md |
| L |
| v0 |
解得:U=1800V,所以,当电压为U2=2000V时,粒子打在上极板
此时:W=q(
| U2 |
| 2 |
答:(1)带电粒子的电量为10-11C.
(2)当电压为U1=800V时,粒子离开金属板时的竖直偏转位移为2.3×10-3m.
(3)当电压为U2=2000V时,该电场最终对粒子所做的功为10-8J.
点评:本题带电粒子在重力场与电场的复合场中做类平抛运动,采用运动的分解法研究,只是重力必须考虑.

练习册系列答案
相关题目
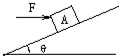 如图,质量m=2.5kg的物体A,在水平推力F的作用下,恰能沿倾角为θ=37°的斜面匀速上滑,g取10m/s2.
如图,质量m=2.5kg的物体A,在水平推力F的作用下,恰能沿倾角为θ=37°的斜面匀速上滑,g取10m/s2.

