Question

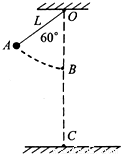
如图所示，让质量m=5.0kg的摆球由图中所示位置A从静止开始下摆，摆至最低点B点时恰好绳被拉断．已知摆线长L=1.6m，悬点O与地面的距离OC=4.0m．若空气阻力不计，摆线被拉断瞬间小球的机械能无损失．求：
（1）摆线所能承受的最大拉力T；
（2）摆球落地时的动能．

Answer 1

分析：（1）由动能定理可以求出摆球由A运动到B时的速度；摆球做圆周运动，在B由牛顿第二定律列方程，可以求出摆线所承受的拉力．
（2）摆线断裂后，摆球做平抛运动，只有重力做功，由动能定理可以求出摆球落地时的动能．

解答：解：（1）设摆球运动到最低点时的速度为v，
以摆球为研究对象，从A到B的过程中，
由动能定理得：mgL（1-cos60°）=

1

2

mv²-0，
摆球做圆周运动，在B点，
由牛顿第二定律得：T-mg=m

v2

L

，
解得：T=100N，v=4m/s；
（2）从绳子断裂到摆球落地过程中，
由动能定律得：mg（OC-L）=E_k-

1

2

mv²，
解得：E_k=160J；
答：（1）摆线所能承受的最大拉力为100N．
（2）摆球落地时的动能为160J．

点评：对物体正确受力分析，明确物体运动过程，应用动能定理即可正确解题．