题目内容
【题目】如图所示,两条“∧”形足够长的光滑金属导轨PME和QNF平行放置,两导轨间距L=1 m,导轨两侧均与水平面夹角α=37°,导体棒甲、乙分别放于MN两边导轨上,且与导轨垂直并接触良好。两导体棒的质量均为m=0.1 kg,电阻也均为R=1 Ω,导轨电阻不计，MN 两边分别存在垂直导轨平面向上的匀强磁场,磁感应强度大小均为B=1 T。设导体棒甲、乙只在MN两边各自的导轨上运动,sin37°=0.6,cos37°=0.8,g取10 m/s2。
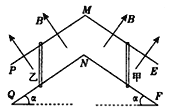
（1）将乙导体棒固定,甲导体棒由静止释放,问甲导体棒的最大速度为多少?
（2）若甲、乙两导体棒同时由静止释放,问两导体棒的最大速度为多少?
（3）若仅把乙导体棒的质量改为m'=0.05 kg,电阻不变,在乙导体棒由静止释放的同时,让甲导体棒以初速度v0=0.8 m/s沿导轨向下运动,问在时间t=1 s内电路中产生的电能为多少?
【答案】（1）
（2）
（3）
【解析】(1)将乙棒固定，甲棒静止释放，则电路中产生感应电动势
感应电流
,甲棒受安培力
甲棒先做加速度减小的变加速运动，达最大速度后做匀速运动，此时
联立并代入数据解得甲棒最大速度
(2)甲、乙两棒同时静止释放，则电路中产生感应电动势
感应电流
，甲、乙两棒均受安培力
最终均做匀速运动，此时甲（或乙）棒受力
联立并代入数据解得两棒最大速度均为
(3)乙棒静止释放，甲棒以初速度
下滑瞬间，则电路中产生感应电动势
感应电流
、甲、乙两棒均受安培力
对于甲棒，根据牛顿第二定律得： 
对于乙棒，根据牛顿第二定律得： 
代入数据联立解得： 
甲棒沿导轨向下，乙棒沿导轨向上，均做匀加速运动
在时间t=1s内，甲棒位移
，乙棒位移
甲棒速度
，乙棒速度
据能量的转化和守恒，电路中产生电能
联立并代入数据解得E=0.32 J
