题目内容
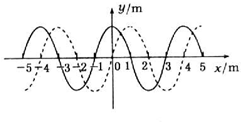
 如图所示,实线是某时刻的波形图线,虚线是0.2s后的波形图线.
如图所示,实线是某时刻的波形图线,虚线是0.2s后的波形图线.(1)若波向左传播,求它传播的最小距离;
(2)若波向右传播,求它的最大周期;
(3)若波速为35m/s,求波的传播方向.
分析:(1)假定波向左传播时,波传播的最短距离为
波长,根据周期性列出波传播的可能距离.
(2)若这列波向右传播,根据周期性得出时间与周期的关系通项式,再求解最大周期.
(3)根据x=υ?△t求出波在0.2s内传播的距离,判断距离与波长的关系即可求解.
| 3 |
| 4 |
(2)若这列波向右传播,根据周期性得出时间与周期的关系通项式,再求解最大周期.
(3)根据x=υ?△t求出波在0.2s内传播的距离,判断距离与波长的关系即可求解.
解答:解:(1)假定波向左传播时,波传播的最短距离为
波长,由图可知波长λ=4m,所以传播的最小距离为xmin=
x=3m.
(2)若这列波向右传播,则有
t=(n+
)T,得
周期T=
,(n=0,1,2…).在所有可能的周期中,当n=0时的最大,故Tmax=0.8s.
(3)若波速为35m/s,在0.2s内传播的距离)△x=υ?△t=35×0.2=7(m)=1
λ,所以波向左传播.
答:(1)若波向左传播,它传播的最小距离为3m;
(2)若波向右传播,它的最大周期为0.8s;
(3)若波速为35m/s,波向左传播.
| 3 |
| 4 |
| 3 |
| 4 |
(2)若这列波向右传播,则有
t=(n+
| 1 |
| 4 |
周期T=
| 4t |
| 4n+1 |
(3)若波速为35m/s,在0.2s内传播的距离)△x=υ?△t=35×0.2=7(m)=1
| 3 |
| 4 |
答:(1)若波向左传播,它传播的最小距离为3m;
(2)若波向右传播,它的最大周期为0.8s;
(3)若波速为35m/s,波向左传播.
点评:本题考查理解波动图象的能力以及运用数学通项求解特殊值的能力.对于两个时刻的波形,有时还要考虑波的双向性.

练习册系列答案
相关题目
 如图所示,实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.
如图所示,实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.